Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовностей.
Приложения:
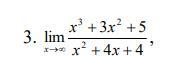

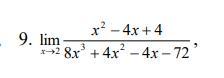
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Оʻzbek tili,
автор: saveliysanin74
Предмет: Алгебра,
автор: parhinsaha05
Предмет: Информатика,
автор: larazzq
Предмет: Другие предметы,
автор: malaya1602