Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Обчислити значення похідних функцій у заданих точках
Вычислить значение производных функций в заданных точках
Приложения:
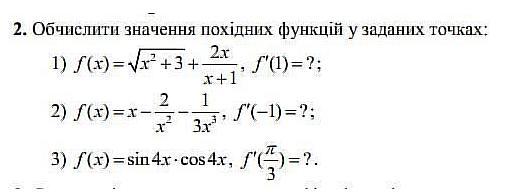
Ответы
Автор ответа:
1
Ответ:
1) 0.5
2) -2
3) -2
Объяснение:
fctdgsygfdhngfxzgsac:
спасибо большое)))
если еще будет возможность помочь, то у меня в профиле есть еще несколько заданий)
https://znanija.com/task/53823433
https://znanija.com/task/53853483
https://znanija.com/task/53859106
https://znanija.com/task/53859115
https://znanija.com/task/53861545
https://znanija.com/task/53823433
https://znanija.com/task/53853483
https://znanija.com/task/53859106
https://znanija.com/task/53859115
https://znanija.com/task/53861545
Похожие вопросы
Предмет: Физика,
автор: sergeystreak13231432
Предмет: Українська мова,
автор: irinahridina2506
Предмет: Математика,
автор: mikhailkurbanov
Предмет: Русский язык,
автор: sarsenovaajganys
Предмет: Алгебра,
автор: kosowaaavekaaa