Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Скласти рівняння дотичної до графіка функції
Составить уравнение касательной к графику функции
Приложения:
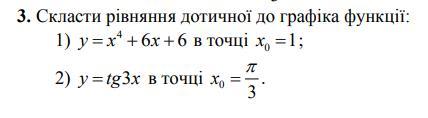
Ответы
Автор ответа:
1
Ответ:
в ответе
Объяснение:
Уравнение касательной имеет вид
, где х₀ - точка касания.
1) y(x) = x⁴ +6x + 6 х₀=1
y'(x) = 4x³ + 6
y(х₀) = (1)⁴ + 6*1 + 6 = 13
y'(х₀) = 4*(1)³ + 6 = 10
уравнение касательной
fctdgsygfdhngfxzgsac:
спасибо большое))
если у Вас будет еще время то у меня еще вопрос есть https://znanija.com/task/53859106
я так понимаю, что я за Вас учусь? -)))))
возможно))
в том вопросе, о котором Вы говорите совсем же табличные производные.......
Похожие вопросы
Предмет: Физика,
автор: egorhtvret
Предмет: Українська література,
автор: pavlenkoa99
Предмет: Математика,
автор: lizaangaraeva58
Предмет: География,
автор: polakovaula575