Предмет: Алгебра,
автор: fctdgsygfdhngfxzgsac
Знайти границі послідовності.
Приложения:
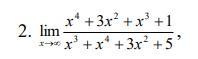
Ответы
Автор ответа:
1
Ответ:
Объяснение:
fctdgsygfdhngfxzgsac:
дуже дякую)
Похожие вопросы
Предмет: Биология,
автор: kokajey
Предмет: Математика,
автор: egornoseleckij2309
Предмет: История,
автор: betsangelina
Предмет: Литература,
автор: pborsakova
Предмет: Русский язык,
автор: darae552