Question

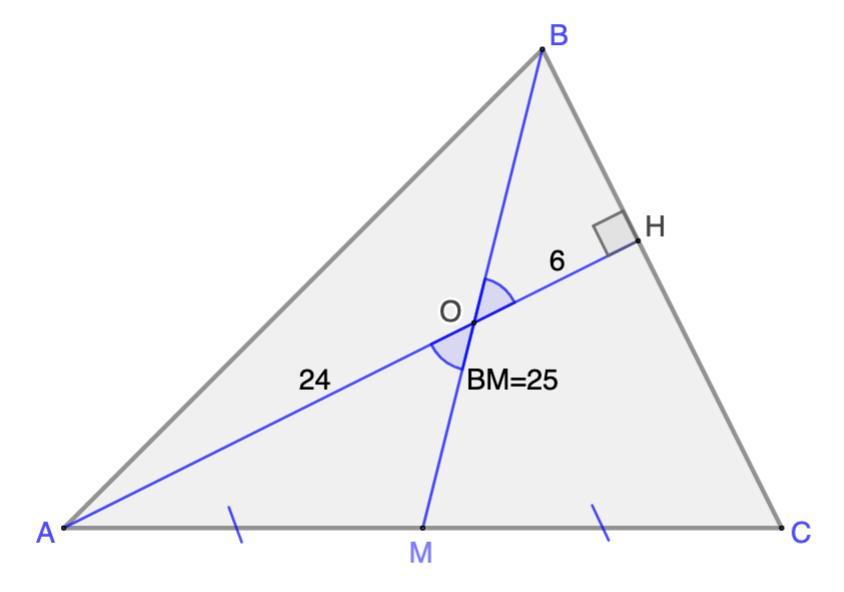
В треугольнике ABC высота AH равна 30, медиана BM равна 25, расстояние от точки пересечения отрезков BM и AH до стороны BC равно 6.
а) Докажите, что BH : CH =1 : 3.
б) Найдите площадь треугольника AMB.

Answer 1

Ответ:

Доказано, что BH : CH =1 : 3;

Площадь треугольника АМВ равна 240 ед.².

Объяснение:

В треугольнике ABC высота AH равна 30, медиана BM равна 25, расстояние от точки пересечения отрезков BM и AH до стороны BC равно 6.

а) Докажите, что BH : CH =1 : 3.

б) Найдите площадь треугольника AMB.

Дано: ΔАВС;

АН = 30 - высота; ВМ = 25 - медиана;

АН ∩ ВМ = О; ОН = 6.

Доказать: ВН : СН = 1 : 3;

Найти: S(АМВ)

Решение:

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ ОН = 6; АО = АН - ОН = 30 - 6 = 24.

Рассмотрим ΔАНС.

ВМ - секущая.

По теореме Минелая:

$\displaystyle \frac{CM}{MA}\cdot\frac{AO}{OH}\cdot\frac{BH}{BC}=1\\ \\ \frac{1}{1}\cdot\frac{24}{6}\cdot\frac{BH}{BC}=1 \;\;\;\Rightarrow \;\;\;\;\;\;\frac{BH}{BC}=\frac{6}{24}=\frac{1}{4}$

⇒ BH : HC = 1 : 3

Рассмотрим ΔМВС.

АН - секущая.

По теореме Минелая:

$\displaystyle \frac{CH}{HB} \cdot\frac{BO}{OM}\cdot\frac{AM}{AC} =1\\\\\frac{3}{1}\cdot\frac{BO}{OM}\cdot\frac{1}{2} =1\;\;\;\Rightarrow \;\;\;\frac{BO}{OM}=\frac{2}{3}$

Пусть ВО = 2х, тогда ОМ = 3х.

2х + 3х = 25  

х = 5

⇒ ВО = 10; ОМ = 15.

Рассмотрим ΔОВН - прямоугольный.

По теореме Пифагора:

ВН² = ОВ² - ОН² = 100 - 36 = 64   ⇒  ВН = 8

Найдем S(АВС).

• Площадь треугольника равна половине произведения высоты на сторону, к которой проведена эта высота.

$\displaystyle S(ABC)=\frac{1}{2}BC\cdot AH\\ \\BH = 8;\;\;\;BH:BC = 1:4;\;\;\;\Rightarrow \;\;\;BC = 32\\\\S(ABC)=\frac{1}{2}\cdot32\cdot30=480$

• Медиана делит треугольник на два равновеликих треугольника.

⇒ S(AMB) = 480 : 2 = 240

Площадь треугольника АМВ равна 240 ед.².

#SPJ1