Question

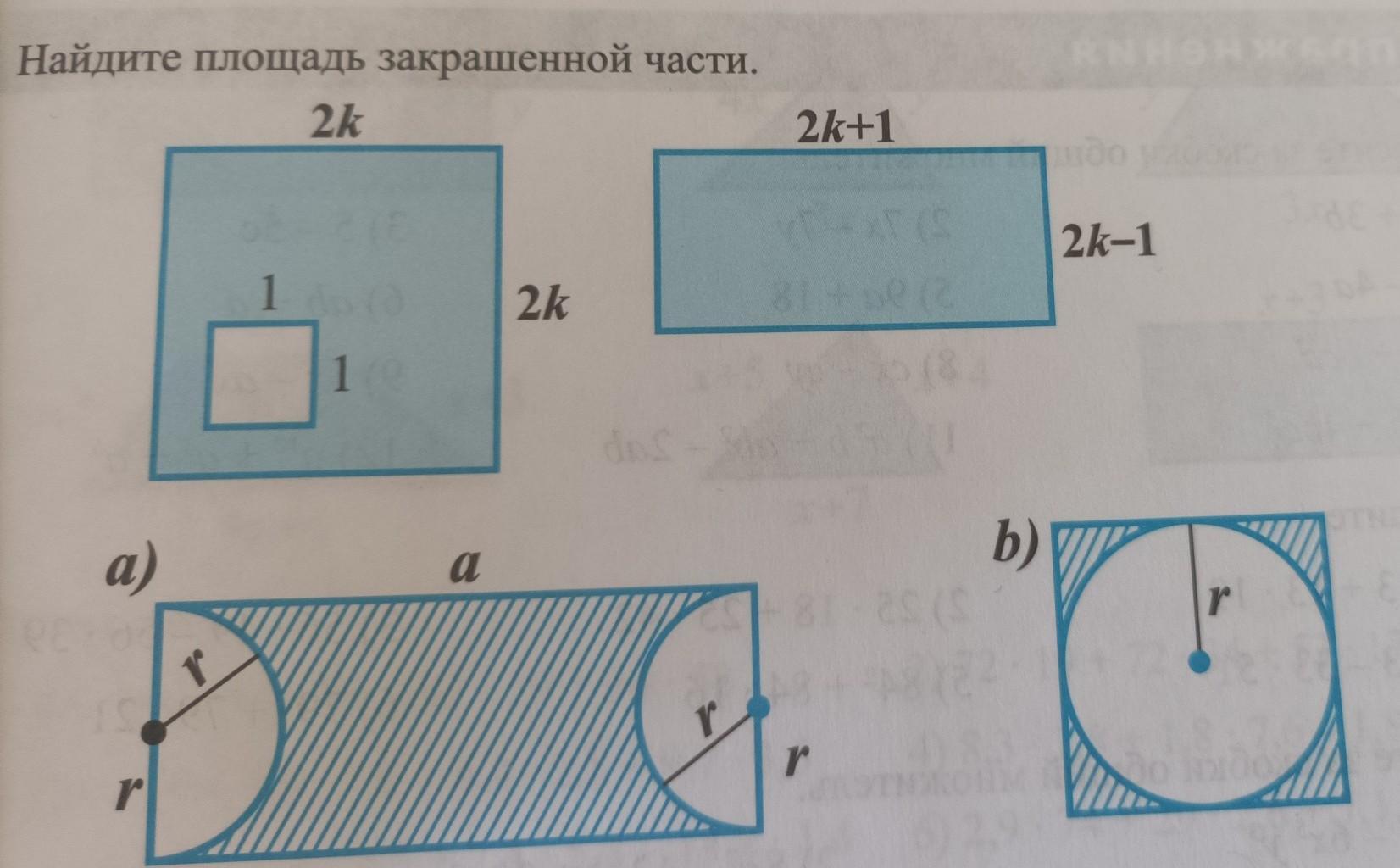
9. Найдите площадь закрашенной части. 2k a) 1 2k 500 + r 2k+1 b) 48124 100 2k-1​

Answer 1

Ответ:

1) Площадь закрашенной части квадрата: S = 4k² - 1.

2) Площадь закрашенного прямоугольника: S = 4k² - 1.

3) Площадь закрашенной части прямоугольника: S = 2ar - πr².

4) Площадь закрашенной части квадрата: S = 4r² - πr².

Пошаговое объяснение:

Найти площадь закрашенной части фигур, изображенных на рисунке.

• Площадь квадрата равна квадрату его стороны.
• Площадь прямоугольника равна произведению его длины на ширину.
• Формула разности квадратов: a² - b² = (a - b)(a + b).
• Площадь круга S = πr²

1) На первом рисунке изображен квадрат со стороной 2k, из которого вырезан квадрат со стороной 1.

Площадь большого квадрата: S₁ = (2k)² = 4k².

Площадь малого квадрата: S₂ = 1² = 1.

Площадь закрашенной фигуры:

S = S₁ - S₂ = 4k² - 1.

2) На втором рисунке изображен прямоугольник со сторонами 2k + 1 и 2k - 1.

Площадь закрашенного прямоугольника:

(преобразуем по формуле разности квадратов)

S = (2k + 1)(2k - 1) = 4k² - 1

3) На третьем рисунке (он отмечен буквой a) изображен прямоугольник, из которого вырезаны две полуокружности радиуса r.

Длина прямоугольника равна a, ширина равна двум радиусам полуокружности (диаметру).

Площадь прямоугольника S₁ = a · 2r = 2ar.

Две полуокружности составляют круг.

Площадь круга: S₂ = πr²

Площадь закрашенной части прямоугольника:

S = S₁ - S₂ = 2ar - πr²

4) На четвертом рисунке (он отмечен буквой b) изображен квадрат, из которого вырезана вписанная окружность радиуса r.

Сторона квадрата  диаметру окружности, т.е. 2r.

Площадь квадрата S₁ = (2r)² = 4r².

Площадь круга: S₂ = πr²

Площадь закрашенной части квадрата:

S = S₁ - S₂ = 4r² - πr².