Question

СРОЧНО!!

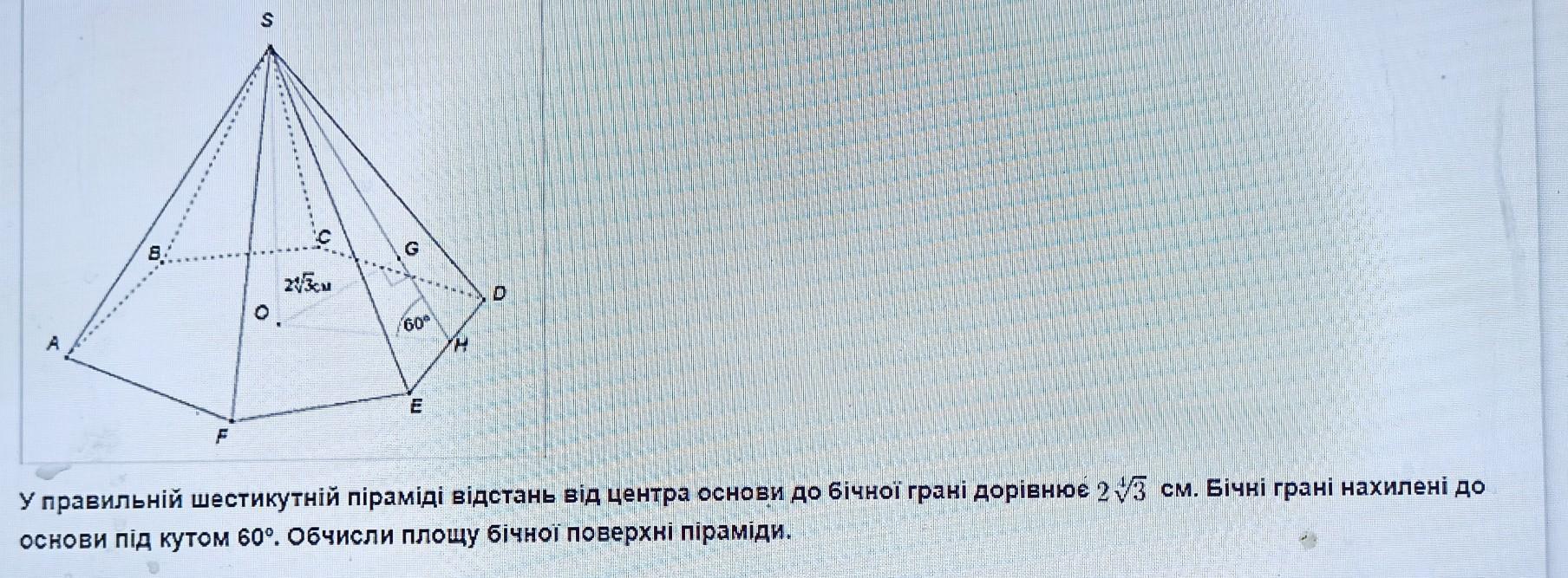
У правільній шестикутній піраміді відстань від центра основам до бічної грані дорівнює 2⁴√3. Бічні грані нахилені до основам під кутом 60°. Обчисліть площу бічної поверхні піраміди.​

Answer 1

Правильная пирамида, боковые грани - равные р/б треугольники.

Найдем сторону основания и высоту боковой грани (апофему).

Опустим апофему SH⊥DE и высоту пирамиды SO⊥осн.

Высота правильной пирамиды падает в центр основания (O).

По теореме о трех перпендикулярах если прямая перпендикулярна наклонной (DE⊥SH), то она перпендикулярна и ее проекции, DE⊥OH.

Угол между плоскостями - угол между перпендикулярами к общей прямой.

∠SHO=60 (угол между боковой гранью SDE и основанием)

Расстояние от точки до плоскости - длина перпендикуляра.

Проведем OG⊥SH.

Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна плоскости и любой прямой в этой плоскости.

DE⊥SH, DE⊥OH => DE⊥(SHO) => DE⊥OG

OG⊥SH, OG⊥DE => OG⊥(SDE)

OG=2⁴√3 (расстояние от центра О до боковой грани SDE)

OH =OG/sin60 =OG 2/√3

ODE - равносторонний (в основании правильный шестиугольник)

DE =OD =OH/sin60 =OG 4/3

SH =OH/cos60 =OG 4/√3

S(SDE) =1/2 DE*SH =OG^2 8/3√3 =4√3 *8/3√3 =32/3

S б.п. =6*32/3 =64