СРОЧНО!! Знайдіть у прямокутника відстань від точки перетину діагоналей до його сторін, якщо периметр прямокутника 72 дм, а одна з його сторін на 4 дм більша за другу.
Ответы
Ответ:
Відстань від точки перетину діагоналей прямокутника до його сторін: 8 дм і 10 дм.
Объяснение:
Знайдіть у прямокутника відстань від точки перетину діагоналей до його сторін, якщо периметр прямокутника 72 дм, а одна з його сторін на 4 дм більша за другу.
1.
- У прямокутника протилежні сторони попарно рівні.
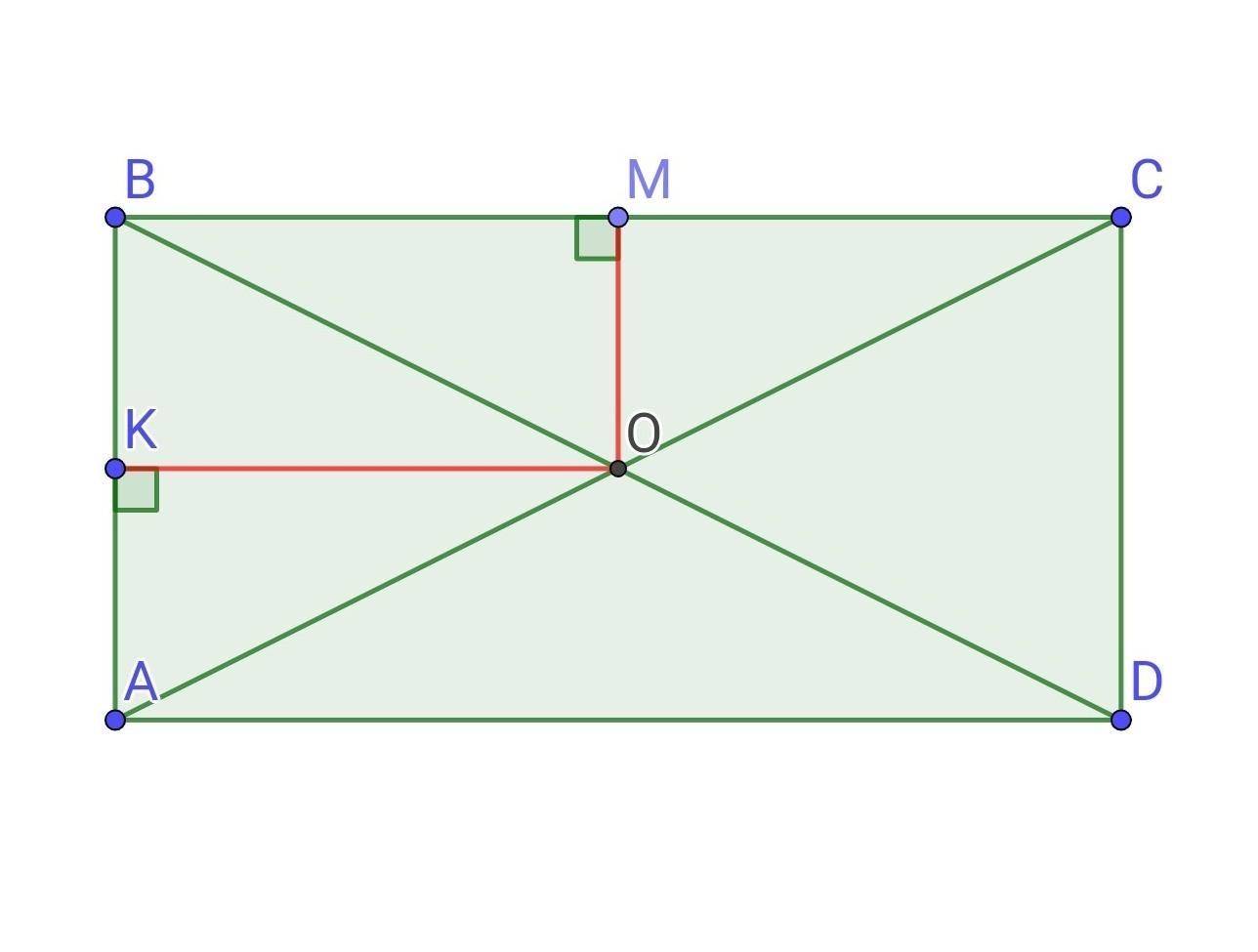
Нехай сторона АВ прямокутника ABCD дорівнює х дм, тоді ВС=(х+4) дм.
Периметр прямокутника знаходять за формулою:
Р=2•(АВ+ВС).
Розв'язуємо рівняння:
2•(х+х+4)=72
2х+4=36
2х=32
х=16.
Отже, АВ = CD = 16 (дм), BC = AD = 16 + 4 = 20 (дм).
2.
AC∩BD=O.
Знайдемо відстань від точки О до сторін AB і ВС.
- Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.
Проведемо перпендікуляри ОК і ОМ до сторін АВ і ВС відповідно.
3.
ОК⟂АВ - за будовою,
ВС⟂АВ - як сторони прямокутника.
Отже, ОК || ВС.
За властивістю діагоналей прямокутника точка О - середина діагоналі АС.
Тоді за теоремою Фалеса точка К - середина сторони АВ. Отже ОК - середня лінія трикутника АВС.
За теоремою про середню лінію:
ОК = ½ • ВС = ½ • 20 = 10 (дм)
4.
ОМ⟂ВС - за будовою,
АВ⟂ВС - як сторони прямокутника.
Отже, ОМ || АВ.
Така як О - середина діагоналі АС, то за теоремою Фалеса точка М - середина сторони ВС. Отже ОМ - середня лінія трикутника АВС.
За теоремою про середню лінію:
ОМ = ½ • АВ = ½ • 16 = 8 (дм)
#SPJ1