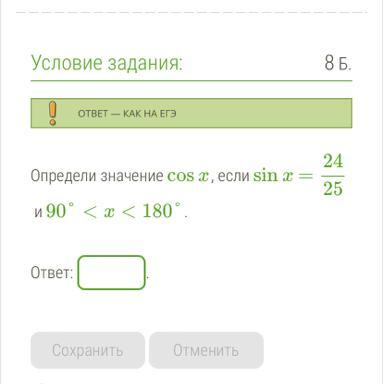
Определи значение cos x, если sin x=
и 90° < x < 180°.
Ответы
Ответ:
Прежде всего, определение значения sin x отсутствует в вашем вопросе, но я предположу, что sin x = a (a обозначает сюда введенное вами значение).
Значения sin x и cos x связаны через тождество sin^2 x + cos^2 x = 1. Используя это, мы можем выразить cos x через sin x следующим образом:
cos x = sqrt(1 - sin^2 x)
Однако sin x и cos x имеют разные знаки в разных квадрантах.
На интервале 90° < x < 180°, x находится во втором квадранте. В этом квадранте cos x отрицателен, тогда как sin x положителен.
Поэтому,
cos x = - sqrt(1 - sin^2 x)
= - sqrt(1 - a^2),
где a - это значение sin x, которое нужно ввести.
Объяснение:
by masterbrainly2023
Ответ:-7/25
Объяснение: Для определения значения cos(x), когда sin(x) = 24/25 и x находится в интервале от 90° до 180°, мы можем использовать тригонометрическую идентичность, связывающую синус и косинус угла.
Идентичность:
sin^2(x) + cos^2(x) = 1
Мы уже знаем значение sin(x), которое равно 24/25. Давайте подставим его в идентичность:
(24/25)^2 + cos^2(x) = 1
Теперь, давайте найдем cos^2(x):
cos^2(x) = 1 - (24/25)^2
cos^2(x) = 1 - 576/625
cos^2(x) = 625/625 - 576/625
cos^2(x) = 49/625
Теперь возьмем квадратный корень с обеих сторон, чтобы найти cos(x), учитывая, что x находится во втором квадранте (90° до 180°), и косинус отрицателен во втором квадранте:
cos(x) = -√(49/625)
cos(x) = -7/25
Таким образом, значение cos(x) в данном случае равно -7/25.