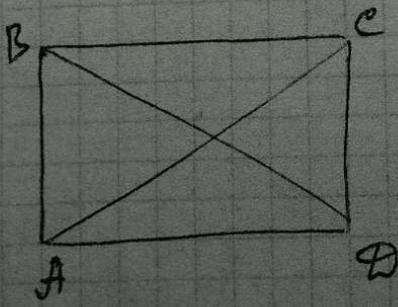
Дано: ABCD-прямокутник, АВ=1/2АС, Знайти кути між АС і ВD
з поясненням прошу!!!
Ответы
Ответ:
В данном случае мы имеем прямоугольник ABCD, где AB равна половине AC. Мы хотим найти угол между AC и BD.
Поскольку AB равно половине AC, для начала мы можем предположить, что AB и BC равны по длине. Тогда AC будет равно корню из суммы квадратов AB и BC, так как у нас есть прямоугольный треугольник ABC.
Теперь мы можем использовать теорему косинусов, чтобы найти угол между AC и BD.
Возьмем угол между AB и AC как θ.
Используя теорему косинусов, мы можем записать:
BD^2 = AB^2 + AD^2 - 2 * AB * AD * cos(θ)
Так как AB = 1/2 AC и AB = BC, мы можем заменить их в уравнении:
BD^2 = (1/4)AC^2 + AD^2 - AC * AD * cos(θ)
Теперь мы можем выразить cos(θ):
cos(θ) = (BD^2 - (1/4)AC^2 - AD^2) / (- AC * AD)
Используя найденное значение cos(θ), мы можем найти сам угол θ с помощью функции обратного косинуса (arccos):
θ = arccos((BD^2 - (1/4)AC^2 - AD^2) / (- AC * AD))
Таким образом, мы можем использовать данную формулу, подставив известные значения сторон AB, AC и длину AD для нахождения угла между AC и BD.