Предмет: Математика,
автор: lowpunq
Найти производную функции. Задание на картинке.
Приложения:
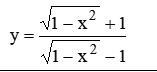
Ответы
Автор ответа:
2
Ответ:
Найти производную дроби .
Формулы : .
Приложения:

Похожие вопросы
Предмет: Математика,
автор: pourur87
Предмет: История,
автор: svedtania2000
Предмет: Математика,
автор: viralusin0
Предмет: Русский язык,
автор: sofa00727