Предмет: Алгебра,
автор: rokfeller007
во вложении....
заданиеС1
Приложения:
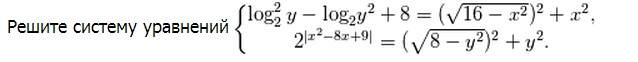
Ответы
Автор ответа:
0
Рассмотрим функцию
Так же
Функция
это вертикальная прямая.
и вторая так же вертикальная прямая
откуда получаем
Автор ответа:
0
ОДЗ неверно указано
Автор ответа:
0
да забыл что логарифм
Автор ответа:
0
и у неверно найден, нам подходит только 1/4
Автор ответа:
0
я быстро решил , вот и ошибки
Автор ответа:
0
Решение на фото, надеюсь видно.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: scoolpolinapolishchu
Предмет: Геометрия,
автор: lydmilasemenova77531
Предмет: Математика,
автор: renthit656
Предмет: Алгебра,
автор: asdddk2jl1