Предмет: Алгебра,
автор: serikesenbaev06
Помогите пожалуйста с заданием
Приложения:
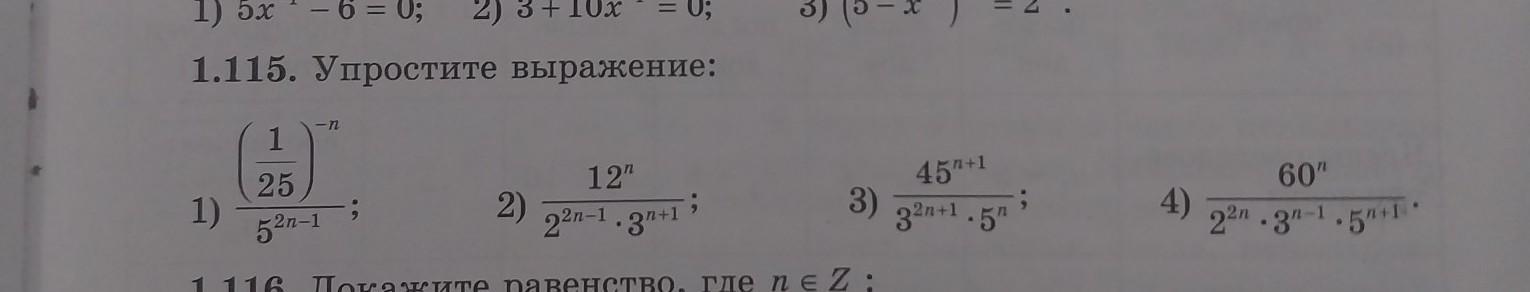
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: pranikschaem
Предмет: Українська мова,
автор: vladpankov678
Предмет: Литература,
автор: uasams0811
Предмет: Химия,
автор: kalbina950
Предмет: Геометрия,
автор: drozdovd34343