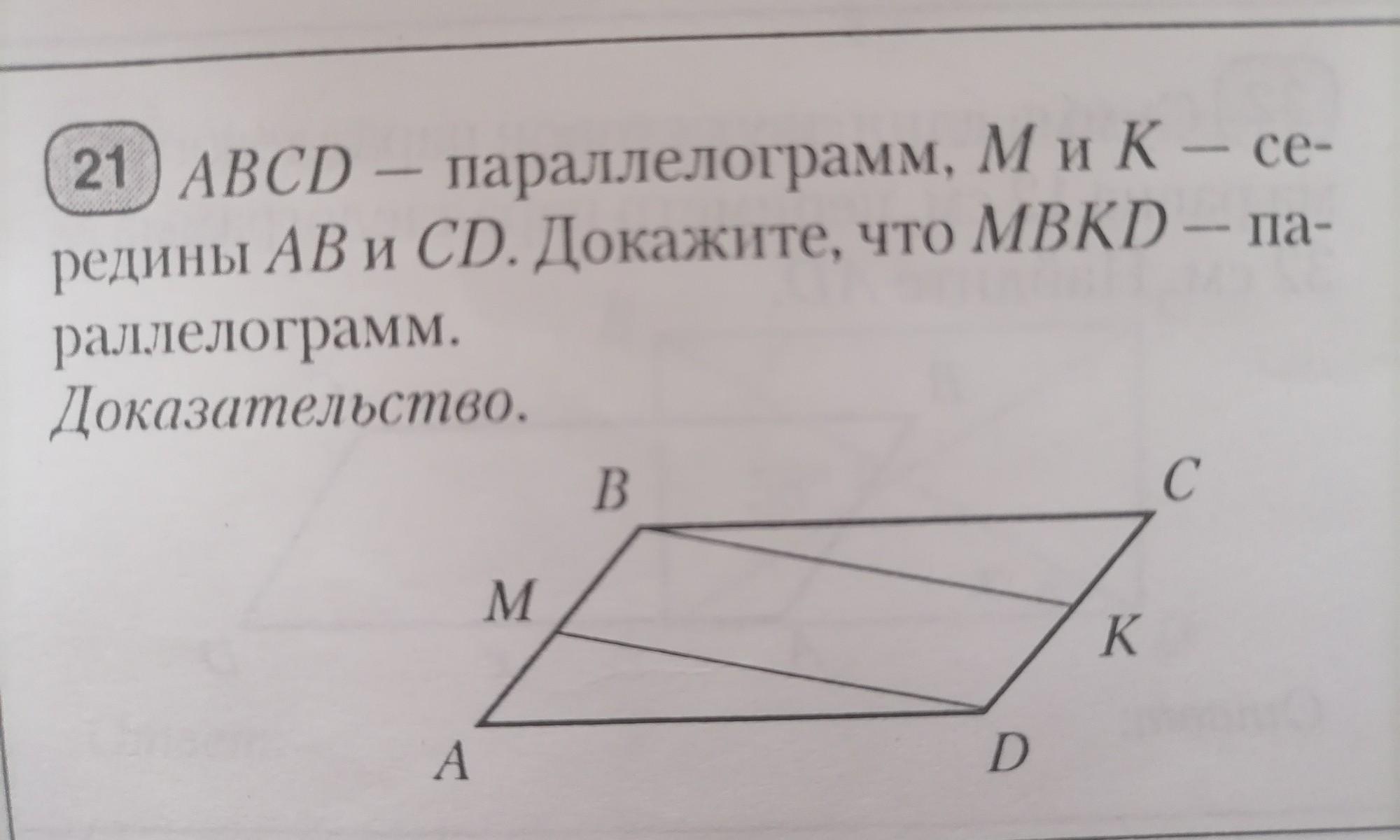
СРОЧНО! ДАЮ 30 БАЛЛОВ ABCD-паралеллограмм, M и K-середины AB и CD. Докажите, что MBKD- паралелограмм.
Ответы
Объяснение:
Для доказательства того, что MBKD - параллелограмм, нужно показать, что его противоположные стороны параллельны.
Давайте рассмотрим параллелограмм ABCD, где M и K - середины сторон AB и CD соответственно.
1. Сначала рассмотрим сторону MB. Поскольку M - середина стороны AB, то MB = MA, и они равны. Также сторона AD параллельна стороне BC (по свойствам параллелограмма). Таким образом, MB параллельна KD, так как обе они параллельны AD.
2. Теперь рассмотрим сторону BK. Аналогично, так как K - середина стороны CD, то BK = KC, и они равны. Также сторона AB параллельна стороне CD (по свойствам параллелограмма). Таким образом, BK параллельна MD, так как обе они параллельны AB.
Таким образом, мы доказали, что стороны MB и KD параллельны (по первому пункту) и что стороны BK и MD параллельны (по второму пункту). Параллельность противоположных сторон - это одно из свойств параллелограмма. Следовательно, MBKD - параллелограмм.
чисел дано не было поэтому текст