Question

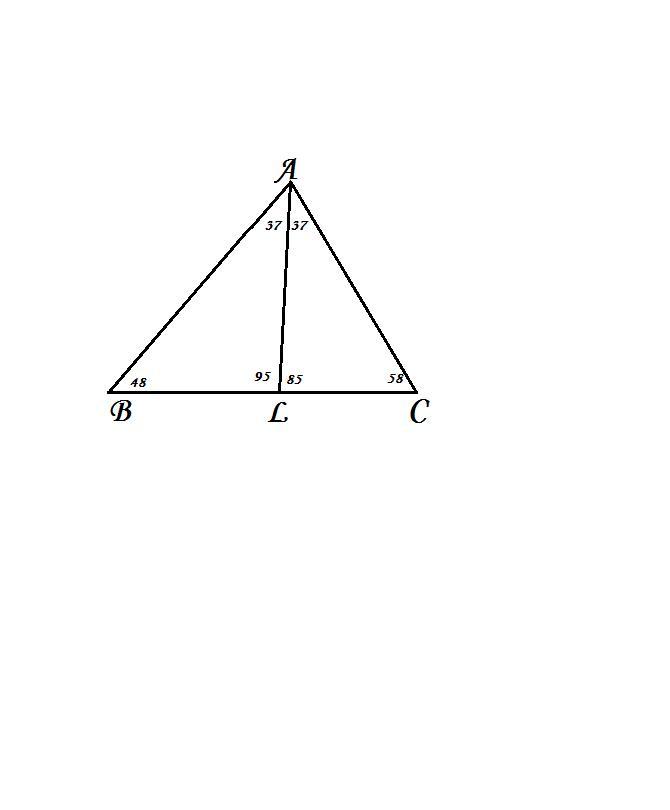
В треугольнике АВС проведена биссектриса AL, угол ALC равен 85°, угол АВС равен 48°. Найдите угол АСВ. Ответ дайте в гра-дусах.

Answer 1

Ответ: 58°

Объяснение:

1.) Сначала найдём величину угла ALB.

CLB - развёрнутый угол.

Значит, CLB = 180°.

CLB = ALC + ALB.

ALB = CLB - ALC.

ALB = 180° - 85°.

ALB = 95°.

2.) Теперь можно найти величину угла BAL.

По правилу сумма величин всех углов в треугольнике равна 180°, то для треугольника LAB можно записать следующее равенство.

LAB + ALB + ABL = 180°.

LAB + 95° + 48° = 180°.

LAB + 143° = 180°.

LAB = 180° - 143°.

LAB = 37°.

3.) Так как по условию AL - это биссектриса, то можно записать следующее равенство.

BAC = 2LAB.

BAC = 2 × 37°.

BAC = 74°.

4.) Теперь найдём величину угла ACB.

Сначала запишем для треугольника ACB равенство, а затем вычислим.

ACB + ABC + BAC = 180°.

ACB + 48° + 74° = 180°.

ACB + 122° = 180°.

ACB = 180° - 122°.

ACB = 58°.

Answer 2

Ответ:

58°

Объяснение:

∠ALB=180-85=95° по свойству смежных углов

∠ВАL=∠CAL=180-48-95=37° по определению биссектрисы

∠АСВ=180-85-37=58°