Предмет: Геометрия,
автор: yavkaske
Дві сторони трикутника дорівнюють 7см і 8см а синус кута між ними  знайдіть третю сторону трикутника
знайдіть третю сторону трикутника
Ответы
Автор ответа:
6
Ответ:
Третья сторона треугольника равна √97 см.
Объяснение:
Две стороны треугольника равны 7 см и 8 см синус угла между ними . Найдите третью сторону треугольника.
Дано: ΔАВС;
АВ = 7 см; АС = 8 см;
Найти: ВС.
Решение:
1 способ.
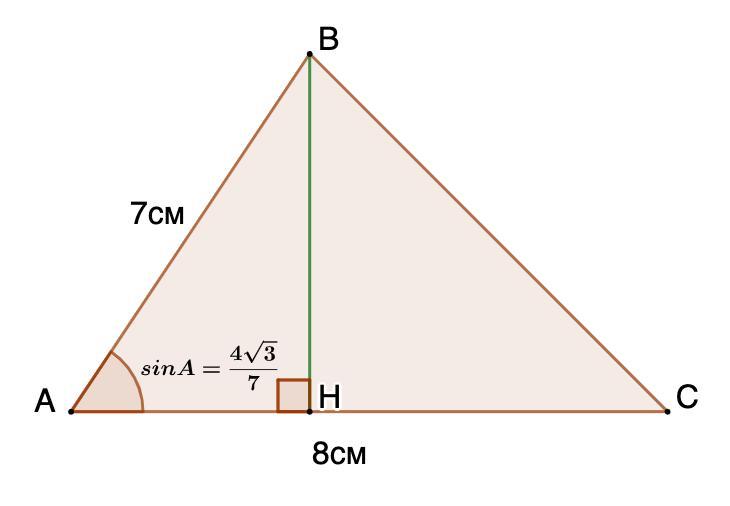
Проведем высоту ВН.
Рассмотрим ΔАВН - прямоугольный.
- Синус угла - отношение противолежащего катета к гипотенузе.
(см)
По теореме Пифагора:
(см)
Рассмотрим ΔНВС - прямоугольный.
НС = АС - АН = 8 - 1 = 7 (см)
По теореме Пифагора:
ВС² = ВН² + НС² = 48 + 49 = 97 ⇒ ВС = √97 см
Третья сторона треугольника равна √97 см.
2 способ.
- Основное тригонометрическое тождество:
sin²α + cos²α = 1
⇒
- Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
BC = √97 (см)
Третья сторона треугольника равна √97 см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Математика,
автор: kstaranova0602
Предмет: Українська література,
автор: tamaraoriginal752
Предмет: Українська мова,
автор: shapovalanna87
Предмет: Математика,
автор: ogoloschapova