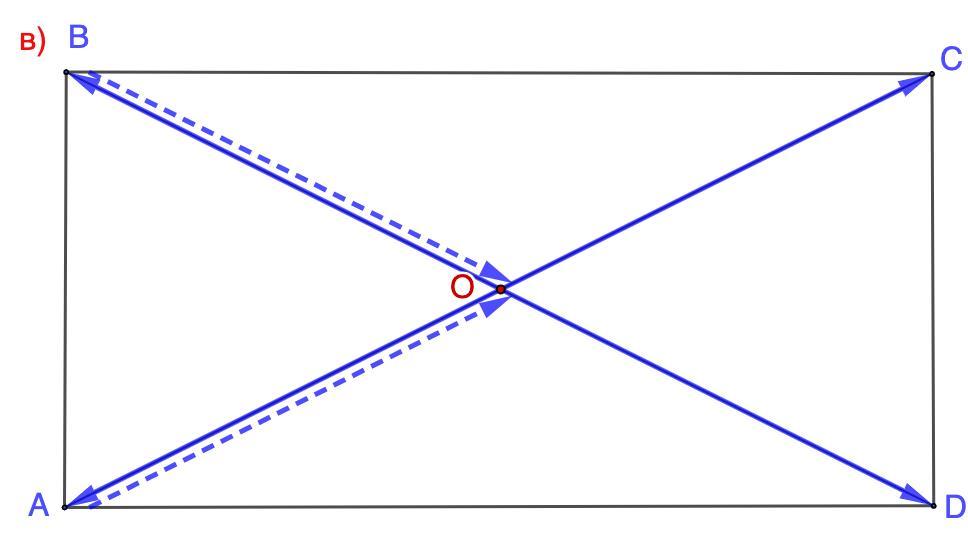
49. в прямоугольнике ABCD диагонали пересекаются в точк O, AB = 2, AD = 4. Найдите: а) |OA + OB \; б) \OA + OB + Oc в) |OA + OB + OC + OD |; x) | AO + DC + OD |.
Ответы
Ответ:
а)
б)
в)
г)
Объяснение:
49. В прямоугольнике ABCD диагонали пересекаются в точке O, AB = 2, AD = 4. Найдите: а) |OA + OB|; б) |OA + OB + OC|; в) |OA + OB + OC + OD|; г) |AO + DC + OD|.
AC и BD - диагонали.
- В прямоугольнике диагонали равны и точкой пересечения делятся пополам.
Рассмотрим ΔАВС - прямоугольный.
По теореме Пифагора найдем АС;
АС² = АВ² + ВС² = 4 + 16 = 20 ⇒ АС = 2√5
⇒ АО = ВО = СО = DO = √5
- Правило сложения векторов:
- Сумма векторов равна вектору, проведенному из начала первого в конец последнего (при последовательном откладывании).
а)
- Векторы называются равными, если они сонаправлены и их длины равны.
Из ΔAOD по правилу сложения векторов:
⇒
б)
От конца вектора ОА откладываем вектор ОС, точка С попадет в точку О. Затем от точки О откладываем вектор ОВ. Суммой векторов будет вектор ОВ.
⇒
в)
Первые три вектора откладываем аналогично пункту б). Затем от точки В откладываем вектор, равный вектору OD. Здесь начало первого вектора совпадает с концом последнего вектора.
⇒
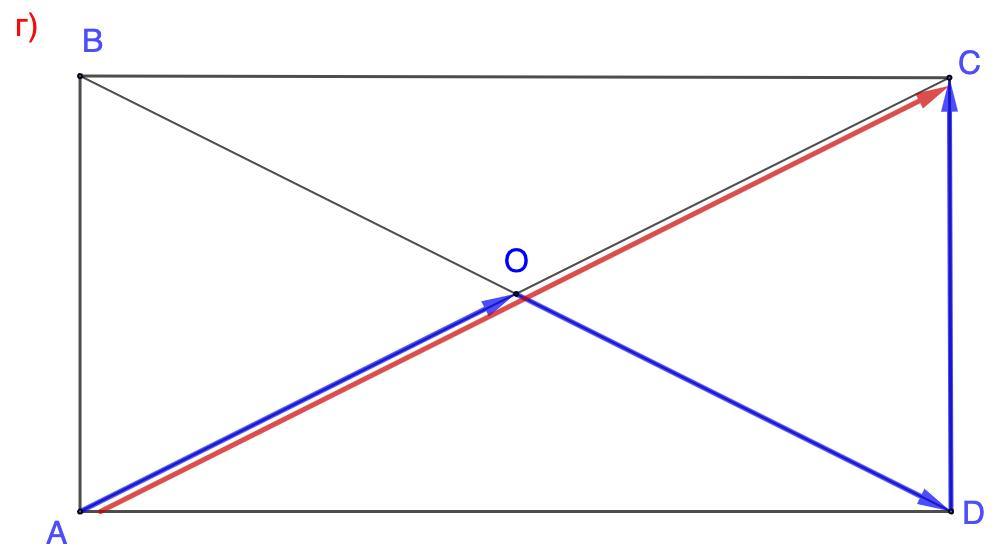
г)
Вектор OD отложен от конца вектора АО, вектор DC отложен от конца вектора ОD. Cуммой векторов будет вектор АС.
⇒
#SPJ1