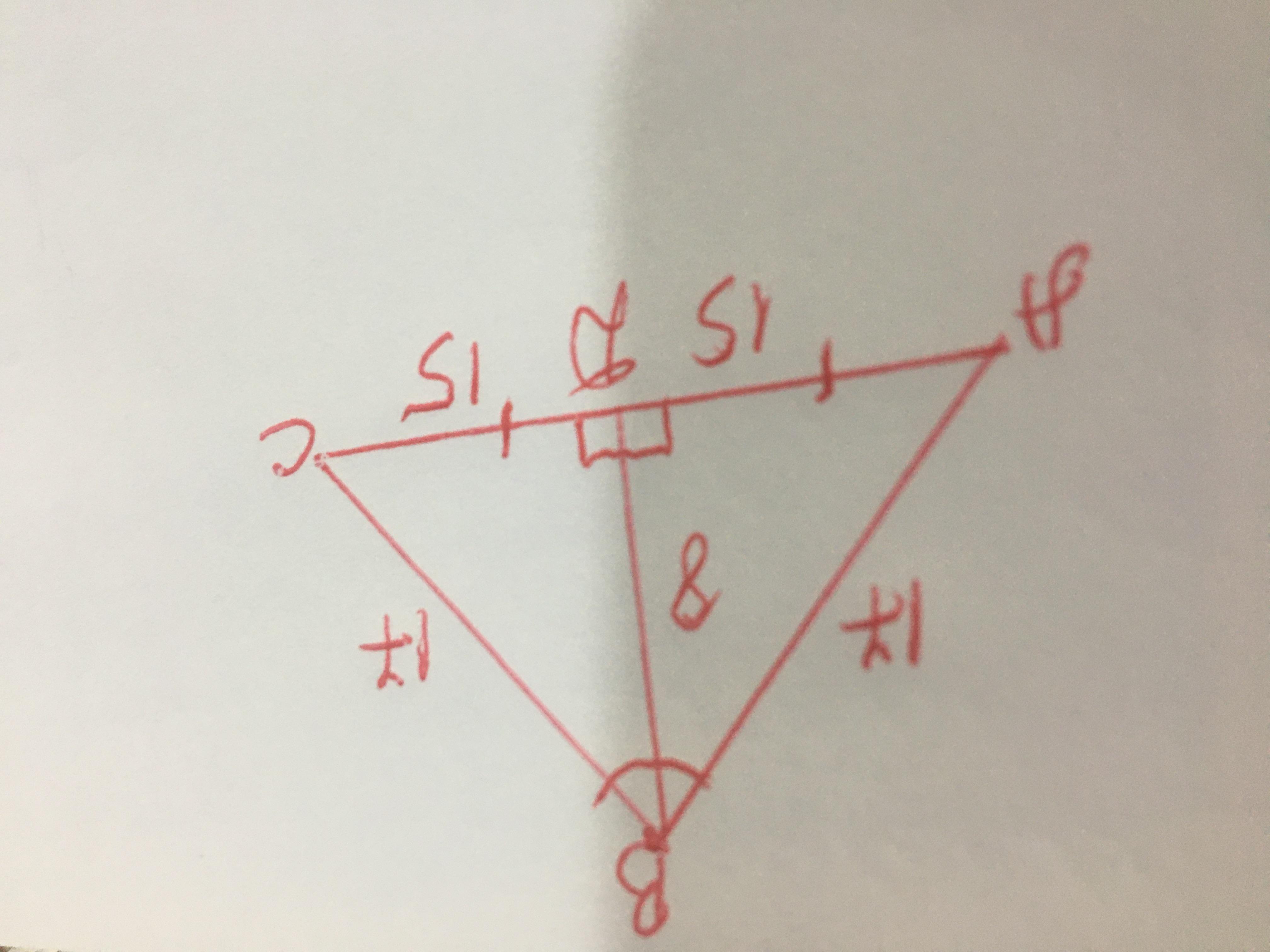
8. Знайти площу трикутника із сторонами 17см, 30 см, 17см.
Помогите пожалуйста решить задание!!
Ответы
Ответ:
Для знаходження площі трикутника зі сторонами 17 см, 30 см і 17 см можна використовувати формулу площі Герона. Спершу знайдемо півпериметр (півсуму сторін):
Півпериметр = (17 см + 30 см + 17 см) / 2 = 64 см / 2 = 32 см
Тепер використаємо формулу Герона для знаходження площі трикутника:
Площа = √[p * (p - a) * (p - b) * (p - c)],
де p - півпериметр, а, b і c - сторони трикутника.
Підставляючи значення, отримуємо:
Площа = √[32 см * (32 см - 17 см) * (32 см - 30 см) * (32 см - 17 см)]
Площа = √[32 см * 15 см * 2 см * 15 см] = √(14400 см²) = 120 см².
Отже, площа цього трикутника дорівнює 120 квадратним сантиметрам.
Ответ:
Треугольник АВС равнобедренный,т к боковые его стороны равны между собой
АВ=ВС=17 см
S АВС=АВ•ВD:2
Найдём ВD
Как уже было сказано-треугольник равнобедренный,в нем ВD-и медиана,и биссектриса,и высота,и делит треугольник АВС на два равных прямоугольных треугольника
Рассмотрим треугольник АВD
По теореме Пифагора найдём ВD
BD^2=AB%2-AD^2
BD^2=17^2-15^2
BD^2=289-225
BD^2=64
Корень квадратный из 64 равен 8
ВD=8 см
S=30•8:2=120 см^2
Объяснение: