ОЧЕНЬ СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ ЗАДАЧУ ПО ГЕОМЕТРИИ!!!!!!!!!!!!!
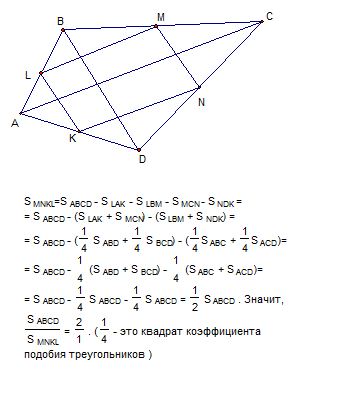
В выпуклом четырехугольнике ABCD отмечены точки K, L, M и N - середины сторон AD, AB, BC и CD соответственно. Найдите отношение площади четырехугольника ABCD к площади четырехугольника KLMN
Ответы
Рассмотрим треугольник АВС. В нем LM - средняя линяя, поэтому S(BLM) = S(ABC)/4 (треугольники АВС и BLM подобны, стороны BLM в 2 раза меньше, значит площадь меньше в 4 раза). Точно так же S(KND) = S(ACD)/4;
Поэтому S(BLM)+ S(KND) = S(AВCD)/4;
Точно так же доказывается что
S(LКА)+ S(МNС) = S(AВCD)/4;
Поэтому
S(BLM) + S(KND) + S(LКА) + S(МNС) = S(AВCD)/2;
Ну, вторая половина остается на долю KLMN :)))
Далее - не принимать всерьез!!!!!
Есть и очень красивое "конвертное" доказательство - если перегнуть все треугольники по средним линиям, как конверт, то они сложатся в такой же параллелограмм:)))) Это уже все решает :)))) (На самом деле это враньё - это работает только для прямоугольников, но для проверки ответа - вполне годится :)))
Кстати, понятно, что KLMN - всегда параллелограмм? :))) для любого выпуклого АВCD.
При решении использован признак подобия треугольников, отношение площадей подобных треугольников.