Question

помогите пожалуйста, дам 40

Answer 1

Ответ:

$\displaystyle f(1)=-12\frac{2}{3}$

Объяснение:

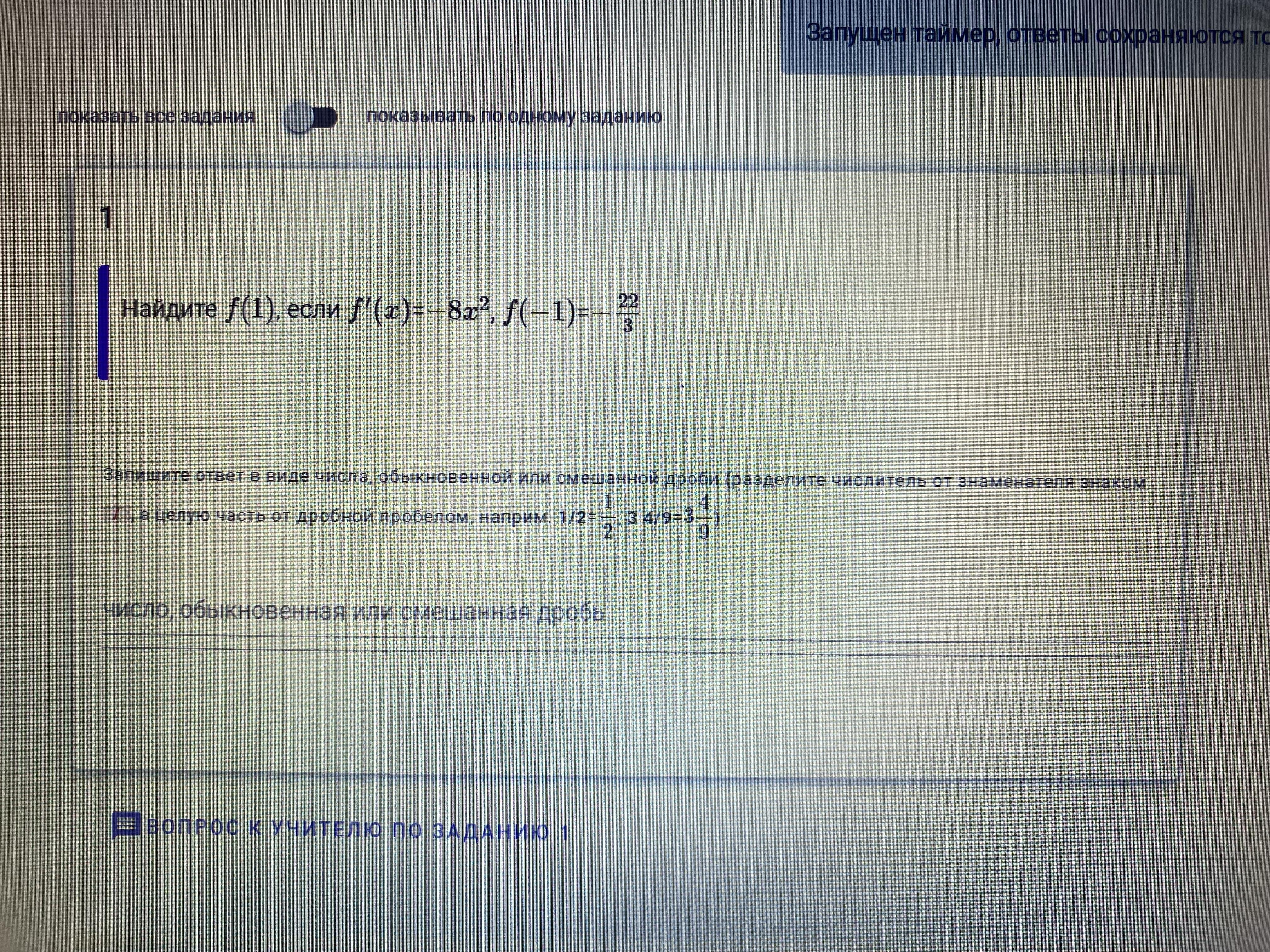
Найдите f(1), если f'(x)=-8x², f(-1)=-22/3

Найдем функцию:

$\displaystyle f(x)=\int\limits {(-8x^2)} \, dx =$

• Постоянный множитель выносится за знак интеграла.

• Интеграл степенной функции:

                $\boxed {\displaystyle \bf \int\limits {x^n} \, dx =\frac{x^{n+1}}{n+1} +C}$

$\displaystyle =-8\int\limits {x^2} \, dx =-8\cdot \frac{x^3}{3}+C=-\frac{8}{3}x^3+C$

Теперь найдем С, используя равенство f(-1)=-22/3

$\displaystyle \bf -\frac{22}{3}=-\frac{8}{3}\cdot (-1)^3+C\\ \\ C=-\frac{22}{3} -\frac{8}{3} \\\\C=-\frac{30}{3}\\ \\C=-10$

Функция примет вид:

$\displaystyle \bf f(x)=-\frac{8}{3}x^3-10$

Теперь найдем f(1):

$\displaystyle f(1)=-\frac{8}{3}\cdot1^3-10=-2\frac{2}{3}-10= \bf -12\frac{2}{3}$