Предмет: Алгебра,
автор: albinansanbaeva456
верно ли что для функции у=f(x) число Т является периодом
Приложения:
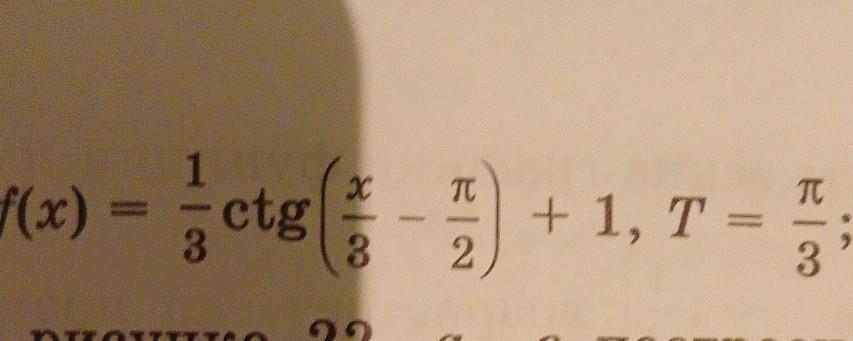
Ответы
Автор ответа:
1
Ответ:
Неверно
Объяснение:
Число T - период функции , а наименьшее положительное значение
T - основной период функции
График функции состоит из бесконечно повторяемых фрагментов графика функции на промежутке [ 0 ; T]. Если функция y = f(x) имеет наименьший положительный период — T, то функция
y = f(kx+b) имеет наименьший положительный период
равный
Период у функции y = ctgx равен π, следовательно период для функции данной по условию будет равен
А значит, что T = π/3 - не является ее периодом
Похожие вопросы
Предмет: Математика,
автор: vovaldyaremko
Предмет: Математика,
автор: daraturenkova362
Предмет: Українська література,
автор: nmarcuk690
Предмет: Математика,
автор: laim7904
Предмет: Геометрия,
автор: svetachornenka95