Question

Обчисліть площу паралелограма, одна зі сторін якого дорівнює 15 см, а діагоналі - 11 см і 25 см.​

Answer 1

Дано :

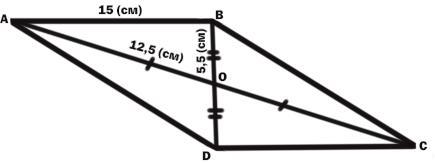
Четырёхугольник ABCD - параллелограмм.

Отрезки АС и BD - диагонали.

Точка О - точка пересечения диагоналей.

АВ = 15 (см).

АС = 25 (см).

BD = 11 (см).

Найти :

S(ABCD) = ?

Решение :

• Диагонали параллелограмма точкой пересечения делятся пополам.

Следовательно -

DO = OB = 11 (см) : 2 = 5,5 (см)

АО = ОС = 25 (см) : 2 = 12,5 (см).

• Диагонали параллелограмма точкой пересечения образуют четыре равновеликих (равных по площади) треугольника.

Отсюда следует, что -

S(ΔABO) = S(ΔBOC) = S(ΔCOD) = S(ΔAOD).

Рассмотрим ΔАВО.

Зная все три стороны треугольника, можно найти его площадь по формуле Герона -

$S = \sqrt{p*(p - a)*(p - b)*(p - c)}$

Где S - площадь треугольника; p - полупериметр треугольника (половина периметра); a, b и с - длины сторон треугольника.

$p(\triangle ABO) = \frac{AB + BO + AO}{2} = \frac{15 + 5,5 +12,5}{2} = \frac{33}{2} = 16,5$ см.

Подставим в формулу Герона -

$S(\triangle ABO) = \sqrt{16,5*(16,5 - 15)*(16,5 - 12,5)*(16,5 - 5,5)}\\\\S(\triangle ABO) = \sqrt{16,5*1,5*4*11}\\\\S(\triangle ABO) = \sqrt{1089}\\\\S(\triangle ABO) = 33$

S(ΔABO) = 33 (cм²).

По выше сказанному -

S(ABCD) = S(ΔABO) + S(ΔBOC) + S(ΔCOD) + S(ΔAOD) = 4*S(ΔABO) = 4*33 (см²) = 132 (см²).

Ответ :

132 (см²).