Question

Знайдіть площю прямокутного трикутника. Якщо гіпотенуза дорівнює 12см, а один з його катетів 5 см а гострий кут 45°.

Answer 1

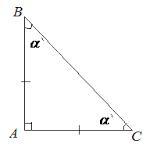
В прямоугольном треугольнике сумма острых углов равна 90°. Допустим ,что угол АСВ=45°

90-45=45(°)- второй острый угол АВС

45°=45° - от сюда следует ,что треугольник равнобедренный . а в нем две стороны ,которые являются катетами, равны. АВ=АС

дальше используем теорему Пифагора .

квадрат гипотенузы равен сумме квадратов катетов

с²=а²+b²

пусть х см катет АВ, тогда катет АС тоже х см

составим и решим уравнение .

12²=х²+х²

2х²=144

х²=144:2

х²=72

х=√72

х=6√2 см -катет АВ .

площадь прямоугольного равнобедренного треугольника равна стороне возведенной в квадрат деленной на два .

S=x²:2 где х сторона

(6√2)²:2=72:2=36 см² - площадь