43. Решите систему неравенств: [6x²-5x+1≤0, Fiora) .
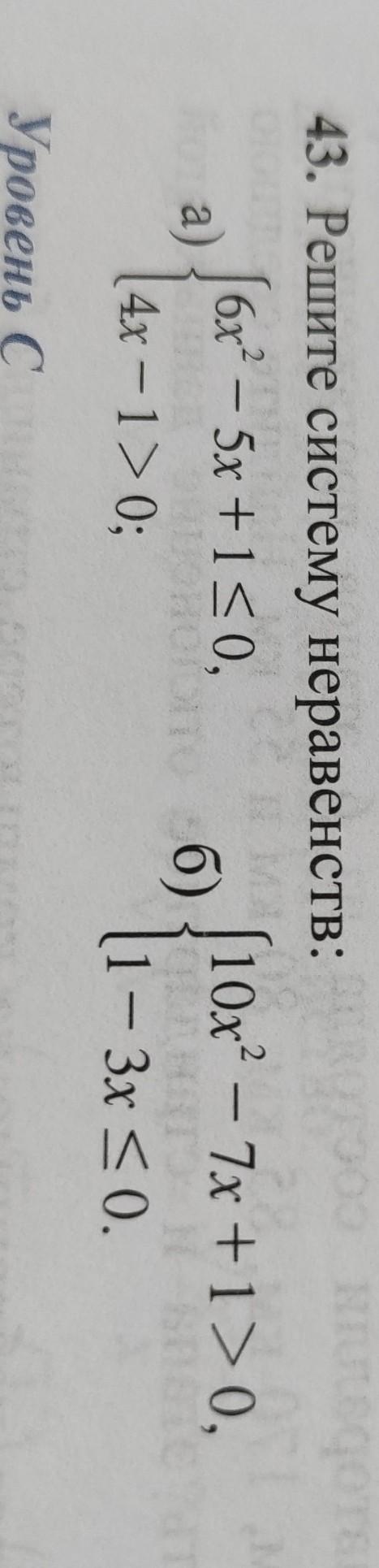
Ответы
Ответ + Пошаговое объяснение:
6x² - 5x + 1 ≤ 0
Сначала найдем корни этого квадратного уравнения:
6x² - 5x + 1 = 0
Для нахождения корней, мы можем использовать квадратное уравнение:
x = (-b ± √(b² - 4ac)) / (2a)
Где a = 6, b = -5 и c = 1. Подставим эти значения:
x = (-(-5) ± √((-5)² - 4 * 6 * 1)) / (2 * 6)
x = (5 ± √(25 - 24)) / 12
x = (5 ± √1) / 12
Теперь найдем два корня:
x₁ = (5 + 1) / 12 = 6/12 = 1/2
x₂ = (5 - 1) / 12 = 4/12 = 1/3
Теперь у нас есть два корня: x₁ = 1/2 и x₂ = 1/3. Давайте построим интервалы на числовой прямой, чтобы определить, когда выражение 6x² - 5x + 1 ≤ 0 истинно.
Интервалы:
1. x < 1/3
2. 1/3 ≤ x ≤ 1/2
3. x > 1/2
Теперь вернемся к исходной системе неравенств. В ней есть только одно неравенство, которое уже мы решили:
6x² - 5x + 1 ≤ 0
Следовательно, ответом на данную систему неравенств будет интервал:
x < 1/3 либо 1/3 ≤ x ≤ 1/2
Это интервалы, в которых неравенство 6x² - 5x + 1 ≤ 0 истинно.