ПОМОГИТЕ МНЕ ПОЖАЛУЙСТА ПОДРОБНО

Ответы
Ответ:
1. AB = 5√2/2 см
2. ∠A = 63°; ∠B = 84°; ∠C = 33°
Объяснение:
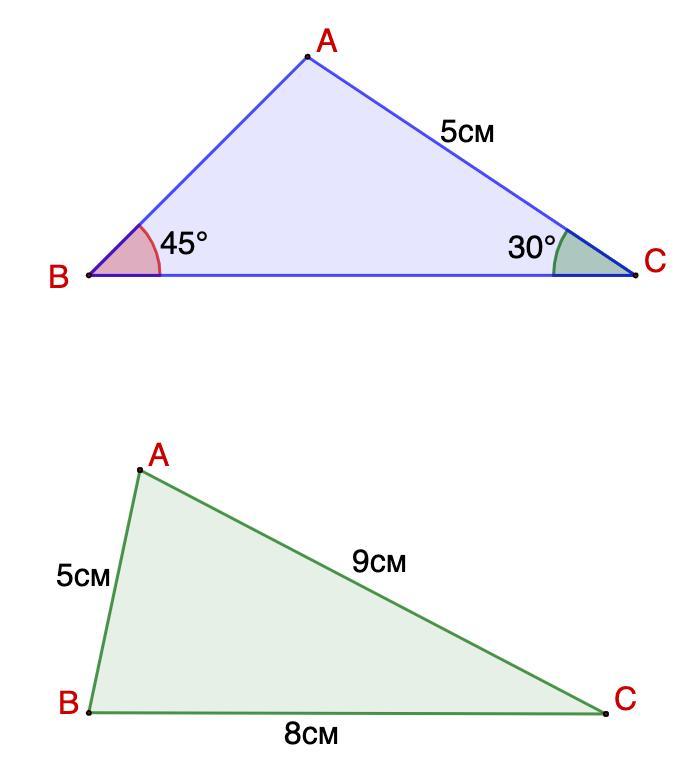
1. В треугольнике АВС известно, что АС = 5 см, ∠B= 45°, ∠C = 30°. Найдите сторону АВ треугольника.
2. В треугольнике АВС известно, что АС = 9 см, АВ = 5 см, ВС= 8 см.
Найдите все углы треугольника.
1. Дано: ΔАВС;
АС = 5 см, ∠B= 45°, ∠C = 30°.
Найти: АВ.
Решение:
- Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов.
2. Дано: ΔАВС;
АС = 9 см, АВ = 5 см, ВС= 8 см.
Найти: ∠А; ∠В; ∠С.
Решение:
- Теореме косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
АС² = АВ² + ВС² - 2АВ · ВС · cosB
81 = 25 + 64 - 2 · 5 · 8 · cosB
80 cosB = 8
По таблице найдем угол:
∠В ≈ 84°
Воспользуемся теоремой синусов:
sin B можем найти при помощи основного тригонометрического тождества:
sin²α + cos²α = 1
⇒ sin²B = 1 - 0,01 = 0,99
sinB = √0,99 ≈ 0,99
∠C ≈ 33°
Сумма углов треугольника равна 180°.
⇒ ∠A = 180° - 84° - 33° = 63°
∠A = 63°; ∠B = 84°; ∠C = 33°
#SPJ1