будь ласка Спростіть вираз:
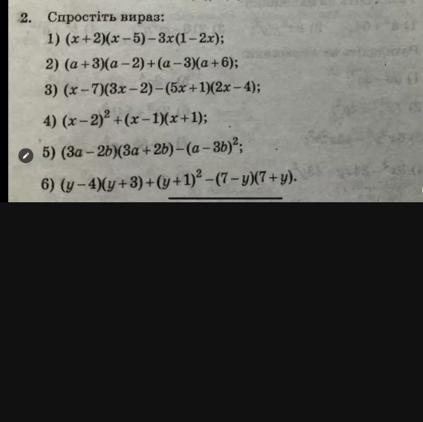
Ответы
Ответ:
1) (x+2)·(x-5)-3·x·(1-2·x) = 7·x²-6·x-10
2) (a+3)·(a-2)+(a-3)·(a+6) = a²+4·a-24
3) (x-7)·(3·x-2)-(5·x+1)·(2·x-4) = -7·x²-5·x+18
4) (x-2)²-(x-1)·(x+1) = -4·x+5
5) (3·a-2·b)·(3·a+2·b)-(a-3·b)² = 8·a²-13·b²+6·a·b
6) (y-4)·(y+3)+(y+1)²-(7-y)·(7+y) = 3·y²+y-60
Объяснение:
Информация. а) Когда требуется перемножить несколько скобок друг на друга, нужно каждый член первой скобки умножить на каждый член второй скобки:
(a+b)⋅(c–d) = a⋅(c–d)+b⋅(c–d) = a⋅c–a⋅d+b⋅c–b⋅d.
б) Формулы сокращённого умножения:
1) (a+b)² = a²+2·a·b+b²;
2) (a-b)² = a²-2·a·b+b²;
3) (a-b)·(a+b) = a²-b².
Решение. Сначала раскроем скобки, потом приведём подобные слагаемые и таким образом упростим выражения.
1) (x+2)·(x-5)-3·x·(1-2·x) = x²-5·x+2·x-10-3·x+6·x² =
= 7·x²+(-5+2-3)·x-10 = 7·x²-6·x-10;
2) (a+3)·(a-2)+(a-3)·(a+6) = a²-2·a+3·a-6+a²+6·a-3·a-18 =
= a²+(-2+3+6-3)·a-24 = a²+4·a-24;
3) (x-7)·(3·x-2)-(5·x+1)·(2·x-4) = 3·x²-2·x-21·x+14-(10·x²-20·x+2·x-4) =
= 3·x²-2·x-21·x+14-10·x²+20·x-2·x+4 = -7·x²+(-2-21+20-2)·x+18 =
= -7·x²-5·x+18;
4) (x-2)²-(x-1)·(x+1) = x²-2·x·2+4-(x²-1) = x²-4·x+4-x²+1 =
= 0·x²-4·x+5 = -4·x+5;
5) (3·a-2·b)·(3·a+2·b)-(a-3·b)² = (3·a)²-(2·b)²-(a²-2·a·3·b+(3·b)²) =
= 9·a²-4·b²-(a²-6·a·b+9·b²) = 9·a²-4·b²-a²+6·a·b-9·b² =
= 8·a²-13·b²+6·a·b;
6) (y-4)·(y+3)+(y+1)²-(7-y)·(7+y) = y²+3·y-4·y-12+y²+2·y+1-(7²-y²) =
= y²+3·y-4·y-12+y²+2·y+1-49+y² = 3·y²+(3-4+2)·y-60 =
= 3·y²+y-60.
#SPJ1