Предмет: Алгебра,
автор: lololllollo
дано многочлени Р(х)=, Q(х)= . Подайте многочлен
Р(х) +Q(х) у канонічному вигляді.
Приложения:
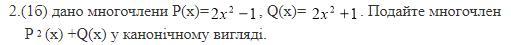
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Математика,
автор: kruykovakaterina2005
Предмет: Право,
автор: mynatelifes
Предмет: Химия,
автор: miroslavkosenko1
Предмет: Физика,
автор: Thecookieking