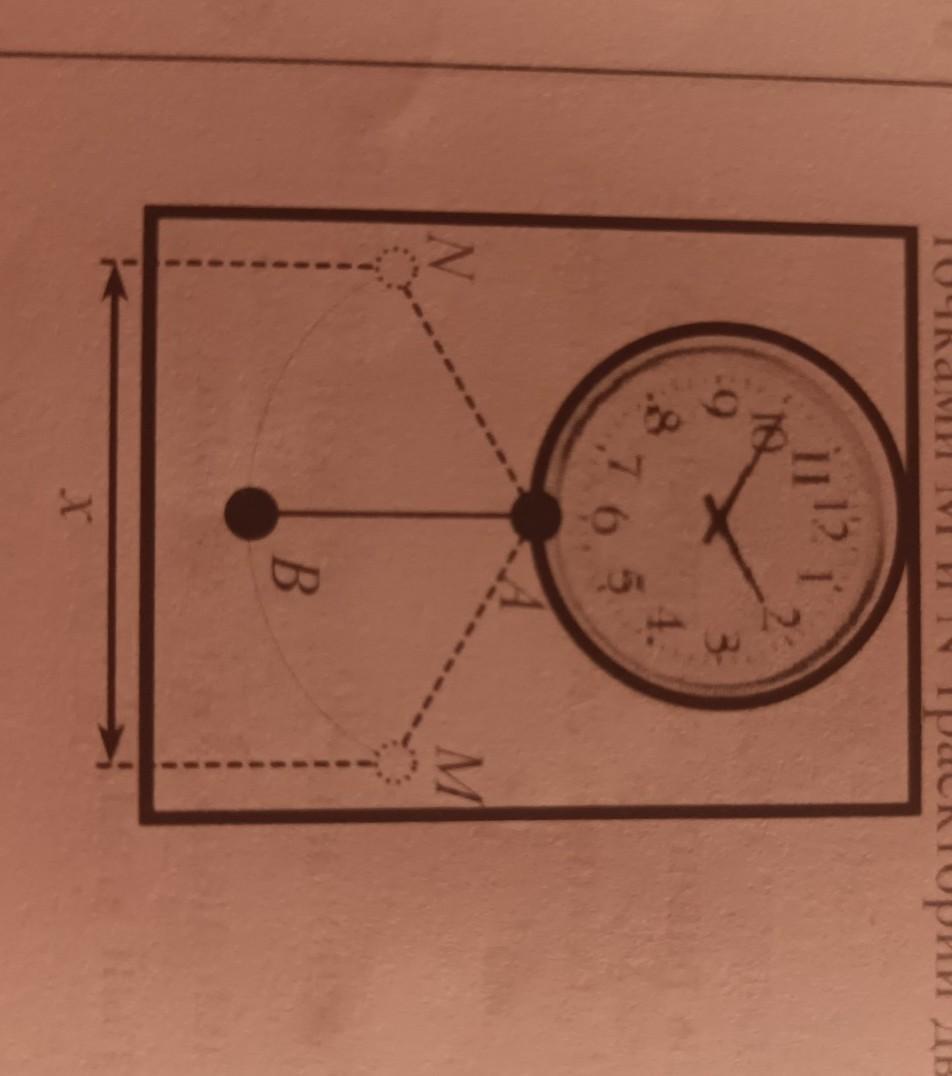
2. На стенных часах маятник АВ, длина которого 15 см, в момент покоя находится на расстоянии 1 см от нижней точки часов. Во время движения наибольшее значение этого расстояния (в точках М и N) может быть равно 7 см. Найдите сколько см составит расстояние между крайними точками М и N траектории движения маятника.
Ответы
Ответ:
Пошаговое объяснение:
Для решения этой задачи мы можем использовать закон сохранения механической энергии. При движении маятника из точки покоя до точек М и N, энергия маятника будет переходить между потенциальной и кинетической формами.
Из консервации энергии, мы можем записать:
максимальное потенциальная энергия = максимальная кинетическая энергия
mgh = (1/2)mv^2
где m - масса маятника, g - ускорение свободного падения, h - высота над точкой покоя, v - скорость маятника.
Между точками М и N, максимальное значение потенциальной энергии будет равно максимальному значению кинетической энергии.
mgh = (1/2)mv^2
Выразим v из этого уравнения:
v = sqrt(2gh)
Разница в высотах между точками М и N равна:
h_разница = h_максимальное - h_минимальное
h_разница = 7 см - 1 см
h_разница = 6 см
Теперь мы можем найти расстояние между крайними точками М и N, используя формулу:
С = 2 * h_разница
С = 2 * 6 см
C = 12 см
Таким образом, расстояние между крайними точками М и N траектории движения маятника составит 12 см.