Предмет: Геометрия,
автор: milenamanuchary
Найдите периметр прямоугольной трапеции, если ее диагональ, равная 20, перпендикулярна боковой стороне, а высота трапеции равна 12.
40 баллов дам. Пожалуйста, с решением, но вот
варианты ответа:
1) 68
2) 75
3) 62
4) 71
5) Среди ответов нет правильного
roown:
1) 68
Ответы
Автор ответа:
1
Ответ: 68 cm
Объяснение:
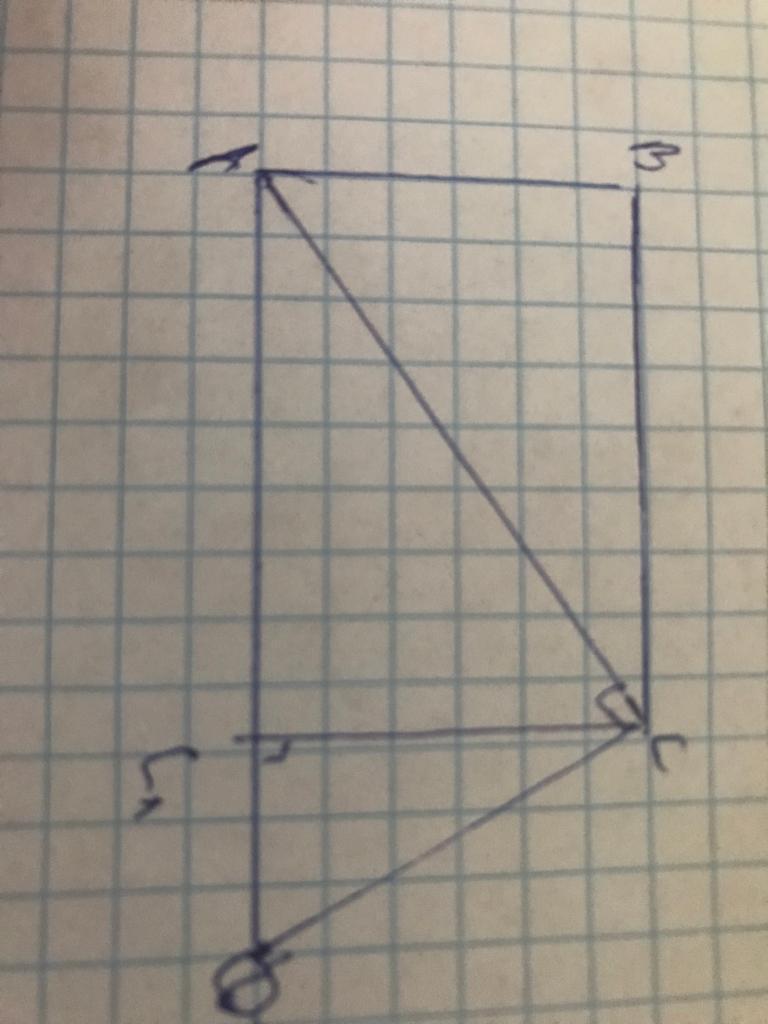
ABCD -данная трапеция.
АС=20
СС1=12 из прямоугольного треугольника АСС1 найдем сторону АС1.
По теореме Пифагора:
по свойству высоты прямоугольного треугольника:
И теперь известны все стороны трапеции, так как AB=CC1
BC=AC1 . AD=AC1+C1D=16+9=25
P=AB+BC+CD+AD=(12+16+15+25)=68 cm
Приложения:
спасибо огромное, вы не представляете, как помогли
Похожие вопросы
Предмет: Математика,
автор: lanakupriyanova1980
Предмет: Українська мова,
автор: liza5797
Предмет: Биология,
автор: polik03
Предмет: Другие предметы,
автор: Villiova
Предмет: Русский язык,
автор: maksimorlov9307