19.5. Найдите периметр прямоугольного треугольника, если его площадь равна S = 5, а высота, опущенная на гипотенузу равна 1.
Ответы
Ответ:
P = √(50 -+ 20√6)(6 ± 2√6) +10 ~= 20.9544511501
Объяснение
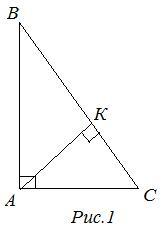
пусть катеты AB = b, AC = a
гипотенуза
S = c* h / 2 => c = 2*S / h = 2 * 5 / 1 = 10
Подобные триугольники ABC ~ KAC по двум углам
BC/AC = AB/KA
10/a = b/1
a = 10/b
Теорема пифагора
a^2+b^2 = c^2
(10/b)^2+b^2 = 10^2
100+b^4 = 100 b^2
b^4 - 100 b^2 + 100 = 0
b^2_{1} =
b^2_{1} =
b^2 = 50 ± 20√6
b = √(50 ± 20√6)
a = 10/b = 10 / √(50 ± 20√6) =
P = b + a + c = b + 10/b + 10 = (b^2+10b + 10) / b = (50 ± 20√6+10√(50 ± 20√6) + 10) / √(50 ± 20√6) = (60 ± 20√6+10√(50 ± 20√6)) / √(50 ± 20√6) = (60 ± 20√6+10√(50 ± 20√6))√(50 -+ 20√6) / √(50 ± 20√6)√(50 -+ 20√6) =
{ √(50 ± 20√6)√(50 -+ 20√6) = √(50^-20^2*6) = √100 = 10 }
= 10 (6 ± 2√6+√(50 ± 20√6))√(50 -+ 20√6) / 10 =
= (6 ± 2√6+√(50 ± 20√6))√(50 -+ 20√6) =
= √(50 -+ 20√6)(6 ± 2√6) +√(50 ± 20√6)√(50 -+ 20√6) =
= √(50 -+ 20√6)(6 ± 2√6) +10 ~= 20.9544511501
Відповідь: 2 способи.
Пояснення:

