Предмет: Геометрия,
автор: zloktor
Задача по геометрии. Помогите решить.
Приложения:
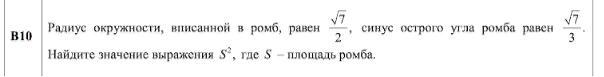
ГАЗ52:
А какой класс?
Мой вариант решения ( без тригонометрии ) : https://ibb.co/3hpB1ZL
p - полупериметр , S =pr - формула площади многоугольника , в который можно вписать окружность
Самое лёгкое объяснение
Нет... Не самое лёгкое.
Самое изящное.
☆☆☆☆☆
Самое изящное.
☆☆☆☆☆
Ответы
Автор ответа:
1
Відповідь:
63
Пояснення:
Приложения:

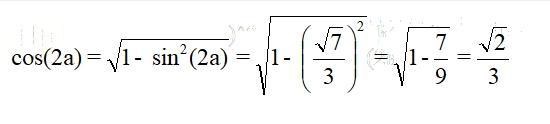
Могли бы объяснить как из синуса двух альфа получить косинус двух альфа? Остальное более менее понятно. Хотя я в шоке. Я думал эта задача решается намного проще. Как я понял площадь находилась основание умноженное на высоту пополам. Тогда зачем там двараза перемножалось r? В общем остались вопросы.
Могли бы объяснить как из синуса двух альфа получить косинус двух альфа? Ещё в формуле площади прямоугольного треугольника не понимаю откуда r*r?
1.формулу для косинуса добавил во вложение
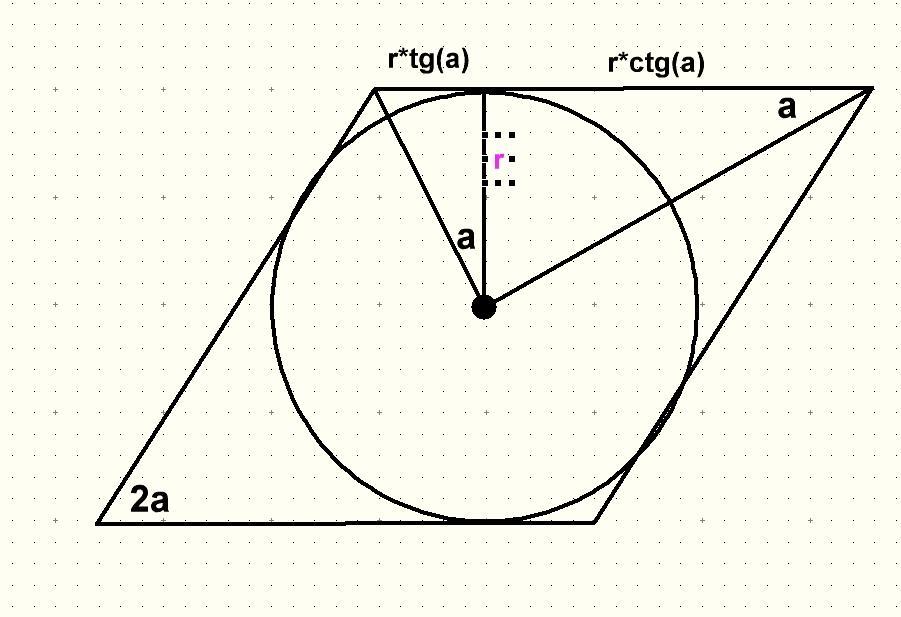
2. площадь треугольника находилась как основание умноженное на высоту пополам. высота это r. основание состоит из двух отрезков.
один из них r*tg(a) второй r*ctg(a)
в итоге площадь ромба это площадь 4 треугольников
S = 4 * (основа * высота /2 ) = 2 * (основа * высота ) =
= 2 * ( r * (tg(a)+ctg(a)) * r ) = 2 * r^2 * (tg(a)+ctg(a))
2. площадь треугольника находилась как основание умноженное на высоту пополам. высота это r. основание состоит из двух отрезков.
один из них r*tg(a) второй r*ctg(a)
в итоге площадь ромба это площадь 4 треугольников
S = 4 * (основа * высота /2 ) = 2 * (основа * высота ) =
= 2 * ( r * (tg(a)+ctg(a)) * r ) = 2 * r^2 * (tg(a)+ctg(a))
Автор ответа:
1
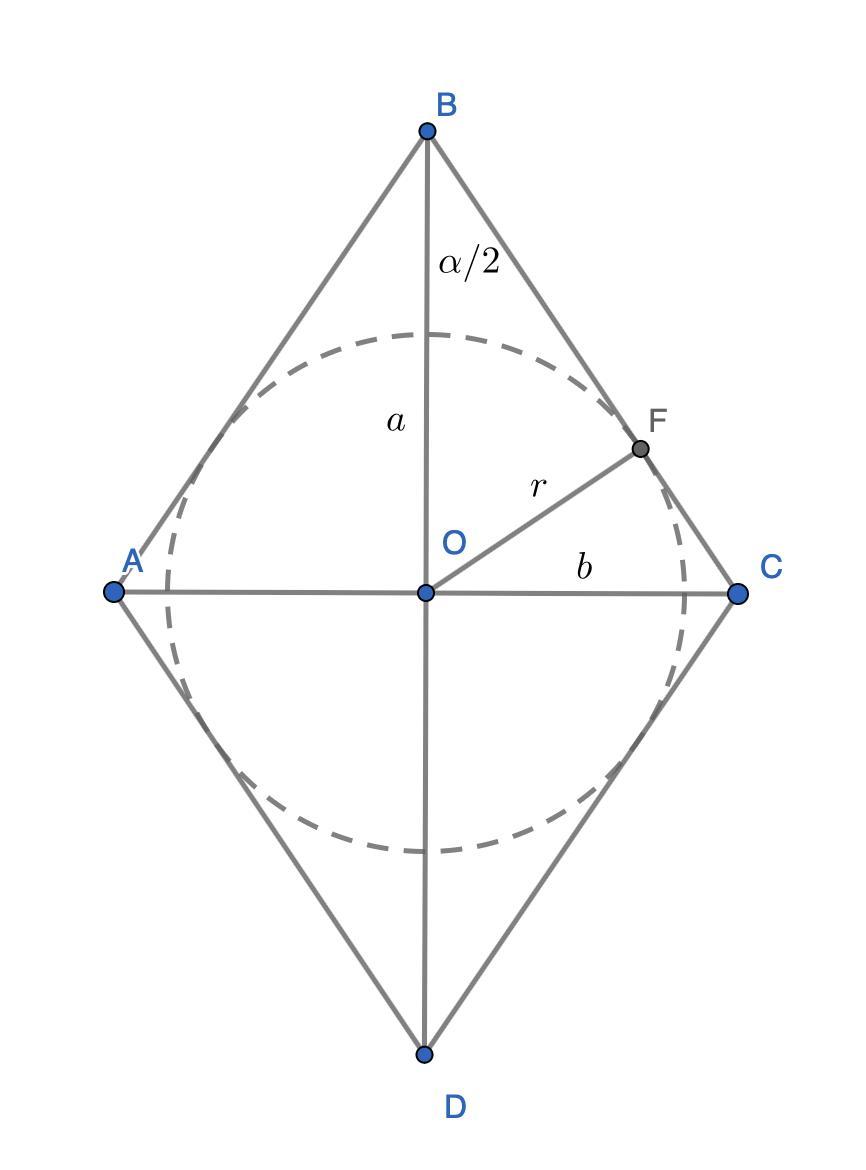
См. рис.
Центр окружности, вписанной в ромб совпадает с центром ромба: точкой пересечения его диагоналей.
Диагонали ромба делят его на 4 одинаковых прямоугольных треугольника. Радиус вписанной окружности является высотой этих треугольников, проведенной из вершины прямого угла.
Один из углов в этих треугольниках, который меньше 45 градусов является половиной острого угла , синус которого равен
Высота в этих прямоугольных треугольниках, которая равна радиусу описанной окружности связана с катетом , который прилежит к углу
следующим образом:
Другой катет
А площадь ромба это 4 таких прямоугольных треугольника с катетами и
Ну и соответственно
Приложения:
Sромба=4•(1/2• a•b)=2 а b.
Ну да, у меня вроде так же
S= 2аb=тут не понял=тут тоже не понял=дальше понятно. Могли бы подробнее эти моменты объяснить?
ну сначала b подставляешь из строчки выше, потом a из строчки еще выше, ну камон
да, я понимаю, но не понимаю как получилось 2 а квадрат тангенс альфа пополам
напишите подробнее решение. Там что-то пропущено.
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Информатика,
автор: lejla4538
Предмет: Українська мова,
автор: cifroua45451
Предмет: Химия,
автор: Sashaklime
Предмет: Химия,
автор: ivan110410pomogite