Question

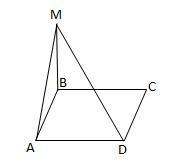
ABCD квадрат, МВ – перпендикуляр, проведений до площини квадрата. Знайдіть довжину сторони квадрата, якщо МВ = 6 см, а похила МD = 10 см

Answer 1

З'єднаємо т. B з т. D, отримаємо відрізок BD.

Оскільки MB перпендикулярна до площини ABCD, то вона є перпендикулярною до будь-якої прямої в цій площині, отже MB перпендикулярна BD.

Тобто трикутник MBD - прямокутний.

В прямокутному трикутнику MBD за Т. Піфагора:

BD^2 = MD^2 - MB^2 = 10^2 - 6^2 = 100 - 36 = 64.

BD = $\sqrt{64}$ = 8(см).

За умовою, ABCD - квдарат, отже його сторона дорівнює

d(діагональ) / $\sqrt{2}$, тобто:

a = d / $\sqrt{2}$ = BD /  $\sqrt{2}$ = 8 /  $\sqrt{2}$ = 4 $\sqrt{2}$(см).

Відповідь: 4 $\sqrt{2}$(см).