Предмет: Алгебра,
автор: valtek10
ДАЮ 100 БАЛЛОВ ЗА 3 ЗАДАНИЕ
Приложения:
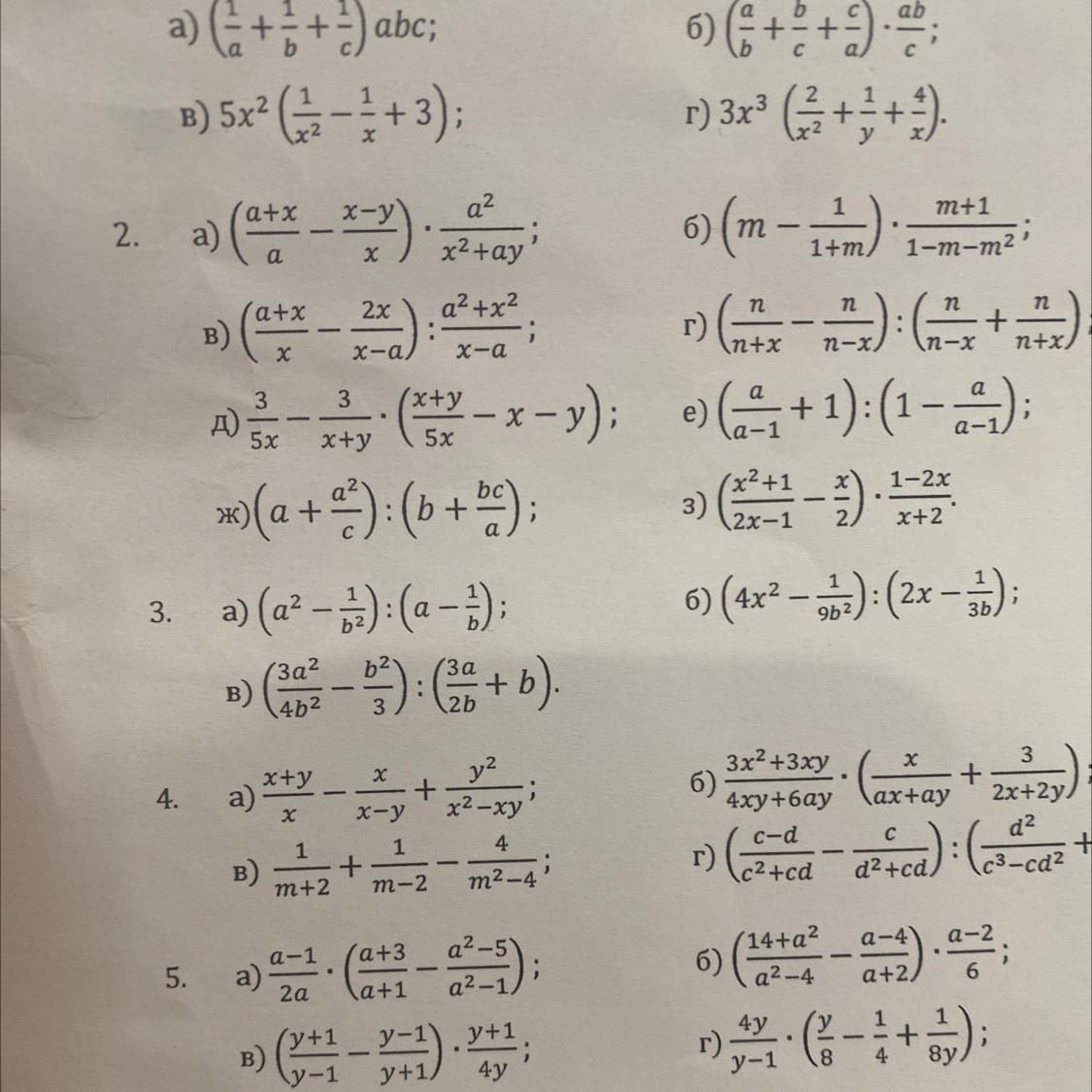
Ответы
Автор ответа:
1
Ответ:
а)
б)
в)
Объяснение:
Упростить выражения:
а)
- В первой скобке используем формулу разности квадратов двух чисел:
a² - b² = (a-b)(a + b)
б)
Решаем аналогично а):
в)
Приведем выражения в скобках к общему знаменателю:
Похожие вопросы
Предмет: Українська мова,
автор: v0487605
Предмет: Информатика,
автор: anastasibro11
Предмет: Математика,
автор: Nastyamoney
Предмет: Математика,
автор: AdamCasper