Предмет: Геометрия,
автор: x29122018
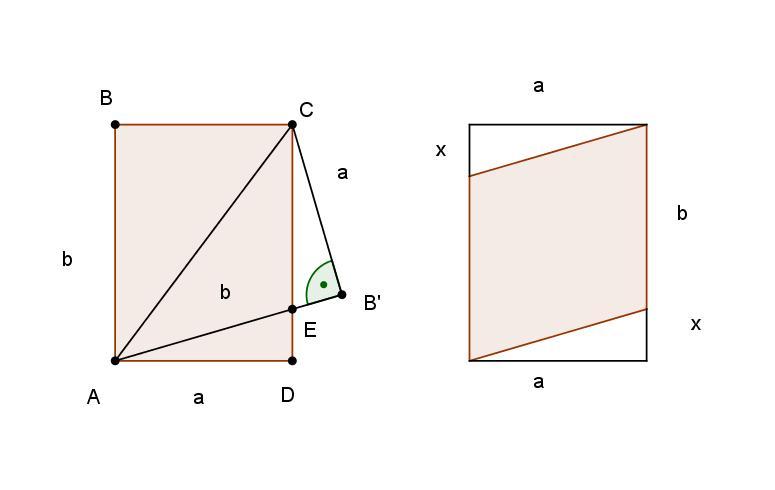
Паперовий прямокутник зі сторонами 3 см і 4 см зігнули по діагоналі. Частини, що виходять за межі двох шарів паперу, відрізали. Знайдіть площу чотирикутника, в який розгортається утворена паперова «фігурка» на фото.
Приложения:

IUV:
9.375
Дякую!
Ответы
Автор ответа:
3
Ответ:
см²
Объяснение:
по теореме Пифагора
площa чотирикутника
Приложения:
Автор ответа:
1
Відповідь: 9 3/8 см²
Пояснення:
ще один спосіб; подібність трикутників.
КО ще легше можна визначити , через tgC і не знадобиться подібність. (див.2 файл).
Точка Н це чисто для побудови симетричного трикутника відносно АС
До речі можна було визначити ВН=2,4. І теж через подібність далі. Способів багато.
Приложения:

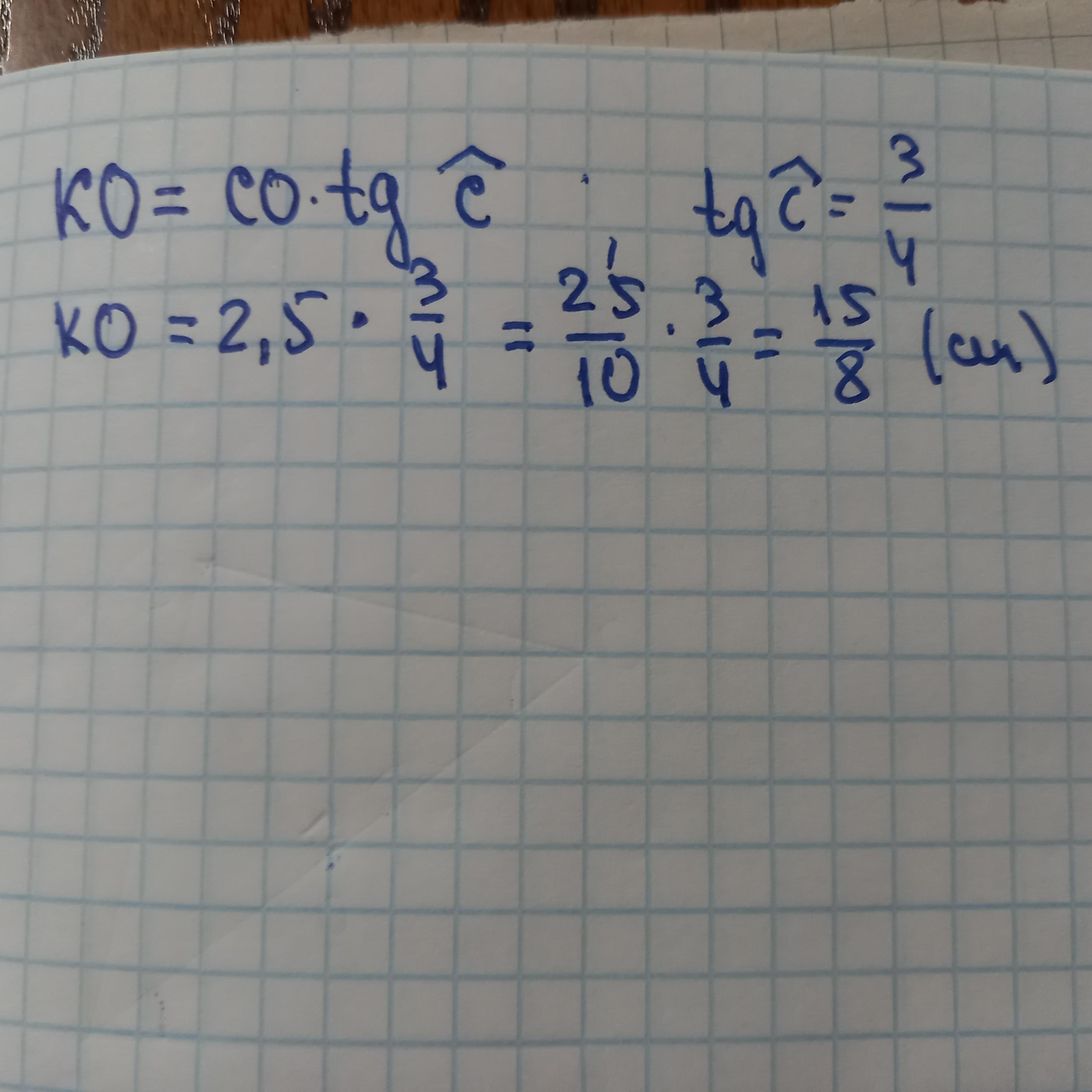
Чи була моя відповідь корисною?
Звичайно
Похожие вопросы
Предмет: Физика,
автор: lemonhelp02
Предмет: Химия,
автор: anyqerw
Предмет: Математика,
автор: Vontix
Предмет: Физика,
автор: lexirimo
Предмет: Геометрия,
автор: sabinashamsid13