Предмет: Алгебра,
автор: khavanskamasha
Терміново!!т Даю сто балів!!! З розвʼязком
Приложения:
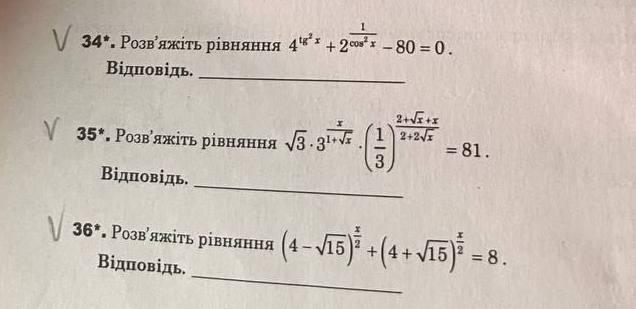
hderyb:
три много, если по одному выложишь то какую-нибудь тебе сделаю
Ответы
Автор ответа:
1
Ответ:
34) Решить уравнение .
Применим формулу:
Замена: ,
35) Решить уравнение .
Применим свойствa степеней : .
36) Решить уравнение .
Основания степеней - взаимно-обратные числа. Убедимся в этом .
Запишем уравнение в виде :
Замена :
Приложения:



бажаю вам міцного здоровʼя
Похожие вопросы
Предмет: Українська мова,
автор: medvidbohdana
Предмет: Физика,
автор: dbvhg
Предмет: История,
автор: iamkaomima
Предмет: Алгебра,
автор: borisenko04
Предмет: Алгебра,
автор: Ela1223