Предмет: Геометрия,
автор: iuvghus
Дан параллелограмм, вершины которого лежат на одной окружности. Найди его меньшую сторону, если соотношение сторон этого параллелограмма 14:48, а радиус окружности — 100 см.
Ответ:
см.
ГАЗ52:
А чертёж был? Чтобы "вершины которого лежат на одной окружности"?
ne bilo
Ответы
Автор ответа:
4
Ответ: 56 cm
Объяснение:
Если вершины параллелограмма лежат на одной окружности, то этот параллелограмм вписан в окружность и такой параллелограмм является прямоугольником.
Причина сумма противоположных углов вписанного 4-х угольника равна 180°, но противоположный углы параллелограмма равны между собой =α=> α+α=180°=> α=90°. α -угол параллелограмма.
Центр описанной вокруг прямоугольника окружности находится на середине его диагонали. => AC= 100·2=200 cm
Обозначим АВ=14x , BC=48x
Тогда по теореме Пифагора имеем
AC²=AB²+BC² => 200²=(14x)²+(48x)²
=> 4 0000=196x²+2304x²
4 0000=2500x²
25x²=400
x=4 cm
=> AB=4·14=56 cm
Приложения:
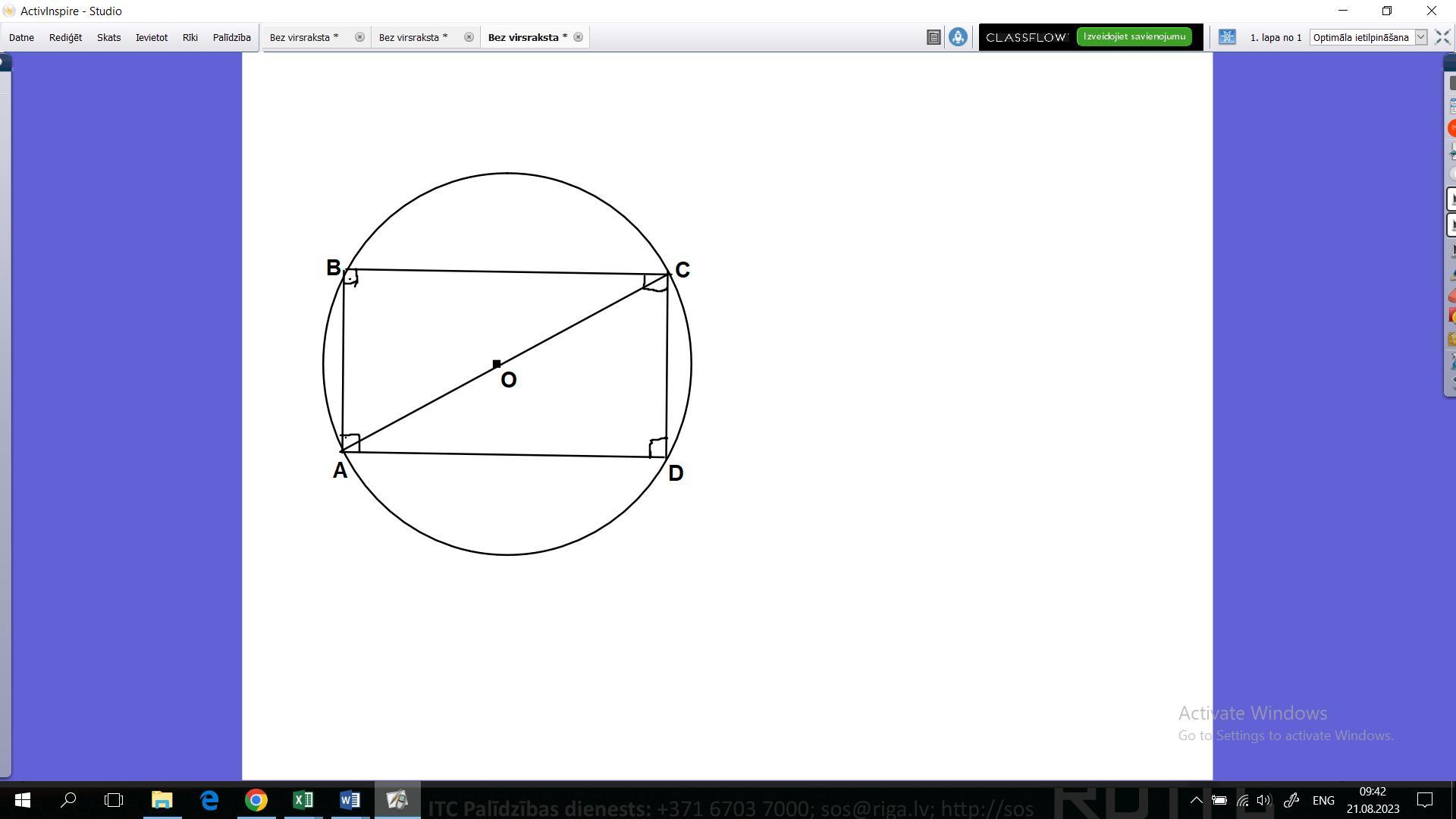
ответ 56 см
там Пифагорова тройка : 7x ; 24x ; 25x ; 25x = 100 ; x =4
только 25х = 200
Похожие вопросы
Предмет: Українська література,
автор: ferenspavel9
Предмет: История,
автор: iamkaomima
Предмет: Английский язык,
автор: iravoloshina231981
Предмет: Математика,
автор: CuBiNsKiY
Предмет: Математика,
автор: sanekbikbulatov