Найти все корни уравнения, не графическим методом !
x² - 17[x] + 60 = 0, []-выделяют целую часть числа не превосходящую само число,
помимо очевидных x = 12, x = 5 найти все остальные решения !
Тут уж буфетчик возмутился.
– Это никому не известно и никого не касается, – ответил он.
– Ну да, неизвестно, – послышался все тот же дрянной голос из кабинета, – подумаешь, бином Ньютона! Умрет он через девять месяцев, в феврале будущего года, от рака печени в клинике Первого МГУ, в четвертой палате."
Ответы
Ответ:
................................................
Объяснение:
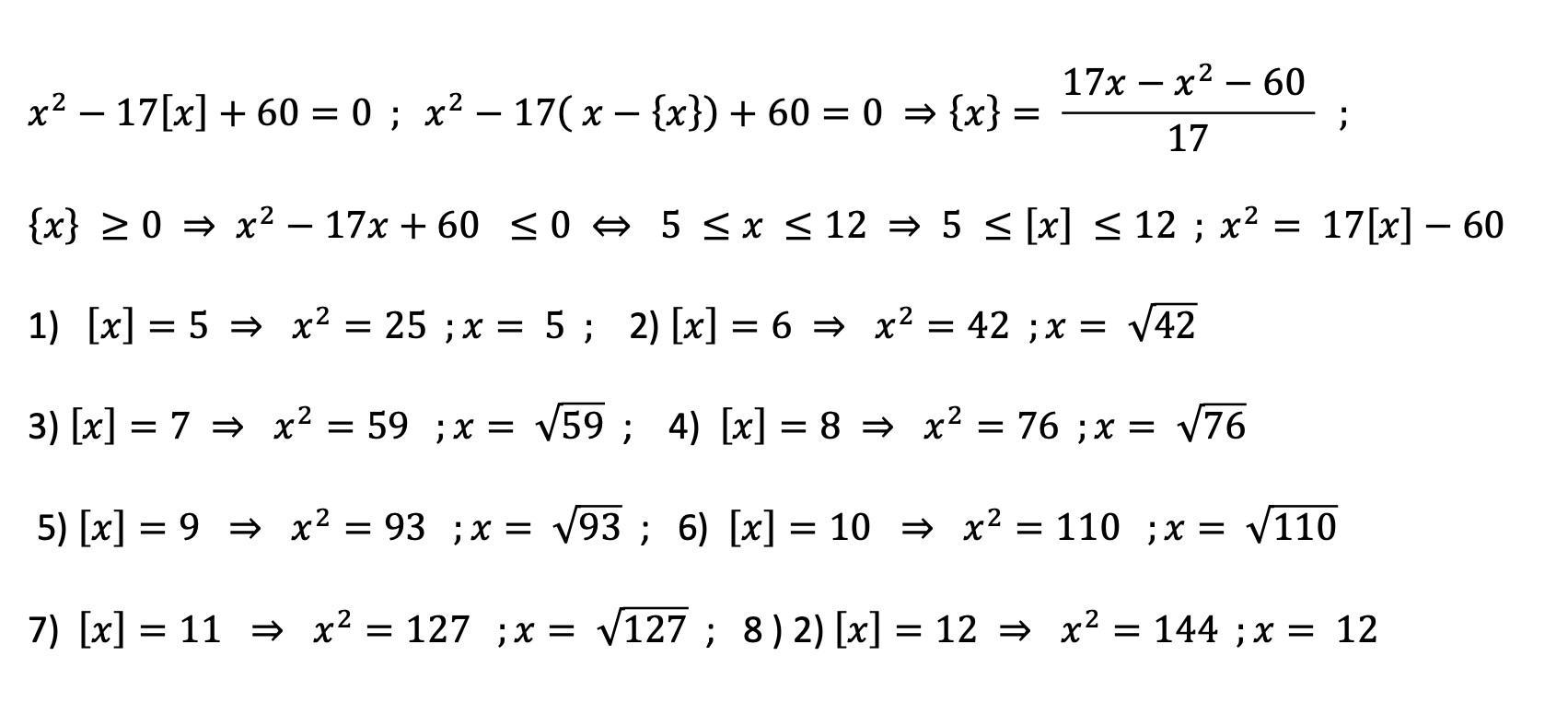
https://znanija.com/task/54023845?utm_source=android&utm_medium=share&utm_campaign=question
1. Рассмотрим случай, когда .
Тогда и, действительно, имеем два корня:
(смысл обозначения второго корня, как восьмого, будет раскрыт ниже).
2. Рассмотрим случай .
Тогда целая часть представима в виде
, где
--- дробная часть числа
.
Перепишем заданное уравнение, используя это соотношение:
Для любого нецелого будет существовать такое
, что
. Тогда
. То есть,
Поскольку рассматриваем , то
.
Первое условие на --- неотрицательность подкоренного выражения:
.
Полученные значения должны попадать в промежуток
:
(доказать равносильность этих неравенств предоставляется читателю). Отсюда получим ещё одно условие:
.
Итого, .
Получим 6 корней:
3. Осталось рассмотреть .
Как я понял из условия, для отрицательных значений функция взятия целой части должна будет вернуть ближайшее целое число, превосходящее заданное по модулю. То есть, например, или
. Поэтому, следует модифицировать найденное в пункте 2 соотношение между функциями
и
.
Рассмотрев пару примеров, нетрудно прийти к соотношению . Подставим его в уравнение:
Аналогично пункту 2, должны иметь натуральное число такое, что
. Тогда
. Получим
Ответ.