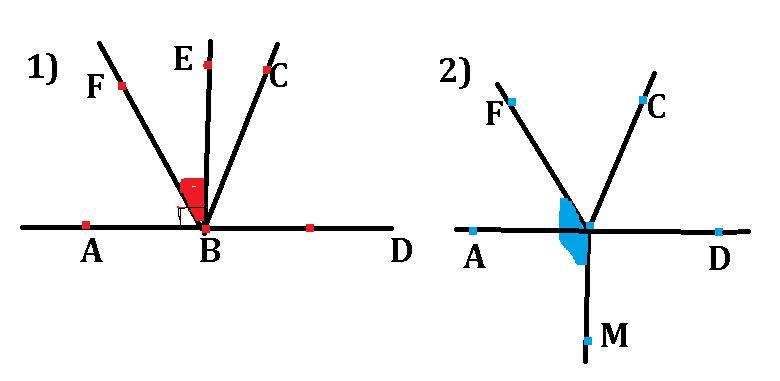
1) Градусні міри суміжних кутів відносяться, як 5:4. Знайдіть градусну міру кута між бісектрисами цих кутів. Скільки розв’язків має ця задача?
Ответы
Объяснение:
5х+4х=180° ,
9х=180°,
х=20°.
Отже АВС = 5×20°=100° , СВD = 4×20° = 80° .

Відповідь:
Дано:
∠ABC i ∠CBD-суміжні.
Градусні міри суміжних кутів ABC i CBD відносяться як 5:4.
Знайти:
градусну міру кута між бісектрисами кутів ABC i ABD. Скільки розв'язків має задача?
Розв'язання:
Нехай ∠ABC = 5х, а ∠CBD=4х, де х - коефіцієнт пропорційності.
сума суміжних кутів дорівнює 180°, тому складаємо рівняння:
5х + 4х =180°; 9х =180°; х = 20°.
Отже, ∠ABC = 5 • 20° = 100°;∠CBD = 4 • 20° = 80°.
1 розв'язання (якщо бісектриси лежать в одній півплощини_:
Нехай BF - бісектриса ∠ABC, BE - бісектриса ∠ABD.
За властивістю бісектриси маємо:
∠ABF = ∠FBC = ∠ABC : 2 = 100° : 2 = 50°,
∠ABE = ∠EBD = ∠ABD : 2 = 180° : 2 = 90°.
За аксиомою вимірювання кутів маємо: (якщо промінь ділить даний кут на два кути, то градусна міра даного кута дорівнює сумі градусних мір двох отриманих кутів)
∠ABE = ∠ABF + ∠FBE
Тоді кут між бісектрисою BF і бісектрисою BE:
∠FBE = ∠ABE - ∠ABF = 90° - 50° = 40°
2розв'язання (якщо бісектриси лежать в різнних півплощинах):
Нехай BF - бісектриса ∠ABC, BМ - бісектриса ∠ABD.
∠ABF = 50°
∠ABM = ∠MBD = ∠ABD : 2 = 180° : 2 = 90° - за властивістю бісектриси.
За аксиомою вимірювання кутів маємо:
∠FBM = ∠ABF + ∠ABM
Кут між бісектрисою BF і бісектрисою BМ:
∠FBM = 50° + 90° = 140°
ВІдповідь:
Задача має два розв'язки. Кут між бісектрисами кутів ABC і ABD дорівнює: 1) якщо бісектриси лежать в одній півплощини, то кут між ними дорівнює 40°;
2) Якщо бісектриси лежать в різних півплощинах то кут між ними дорівнює 140°.
Пояснення: