Предмет: Математика,
автор: Аноним
напишите решение пж
Приложения:

Ответы
Автор ответа:
0
Решение .
Решить систему уравнений . Применим метод сложения .
Ответ: .
Проверкой можно убедиться , что найденные значения х и у удовлетворяют уравнениям системы .
Замечание . В условии , наверное , есть описка .
Приложения:
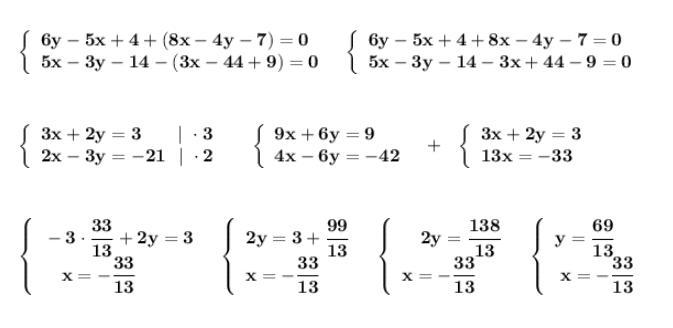
Похожие вопросы
Предмет: Алгебра,
автор: skryzhevska
Предмет: Другие предметы,
автор: Lera89012
Предмет: Литература,
автор: yanqikxx
Предмет: Окружающий мир,
автор: antonbebeley
Предмет: Математика,
автор: bmxer2007german42