Предмет: Алгебра,
автор: Xonda7777
Вычислить неопределенный интеграл
Приложения:
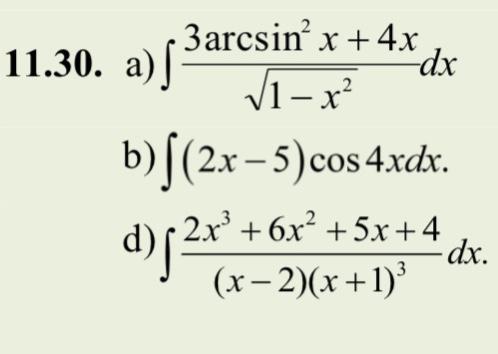
Ответы
Автор ответа:
2
Ответ:
а) Непосредственное интегрирование и подведение под знак дифференциала .
b) Интегрирование по частям : .
d) Интегрирование рациональных дробей .
Найдём коэффициенты методом неопределённых коэффициентов .
Приложения:


Xonda7777:
Спасибо огромное
Похожие вопросы
Предмет: Немецкий язык,
автор: Trlmsqwrf
Предмет: Математика,
автор: angelinamuhankova8
Предмет: Геометрия,
автор: patipez1982
Предмет: Физика,
автор: karobochka125
Предмет: Русский язык,
автор: zitachernyshova