Высоты параллелограмма рав- ны 3 см и 4 см, а его площадь равна 48 см2. Найдите пери- метр параллелограмма.
Ответы
Для нахождения периметра параллелограмма, нам необходимо знать длины его сторон. Однако из условия задачи предоставлены лишь высоты параллелограмма и его площадь. Нам понадобится дополнительная информация для решения задачи.
Если предположить, что высоты перпендикулярны к соответствующим сторонам и пересекаются в точке, то можно применить следующую формулу для площади параллелограмма:
Площадь = высота * основание
где основание - это любая из сторон параллелограмма.
Из условия задачи у нас есть две высоты: h1 = 3 см и h2 = 4 см, а также площадь S = 48 см^2. Предположим, что h1 соответствует основанию b1, а h2 соответствует основанию b2.
Тогда у нас есть два уравнения:
1) S = h1 * b1
2) S = h2 * b2
Подставим значения и решим уравнения относительно оснований:
1) 48 см^2 = 3 см * b1 => b1 = 48 см^2 / 3 см = 16 см
2) 48 см^2 = 4 см * b2 => b2 = 48 см^2 / 4 см = 12 см
Теперь у нас есть длины сторон параллелограмма: b1 = 16 см и b2 = 12 см.
Периметр параллелограмма вычисляется по формуле:
Периметр = 2 * (b1 + b2)
Подставим значения:
Периметр = 2 * (16 см + 12 см) = 2 * 28 см = 56 см
Таким образом, периметр параллелограмма равен 56 см.
Відповідь:
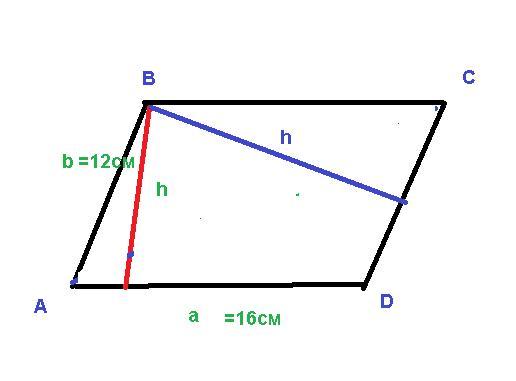
Дано:
параллелограмм АВСD, стороны а и b
Высота h1-3см ; высота h2 -4см
площадь-S-48см2
Найти -периметр-Р-?
Решение:
Площадь параллелограмма равна произведению длины его стороны на высоту, проведенную к этой стороне:
S = a * ha = b * hb.
Зная площадь и обе высоты, можем найти стороны:
a = S / h1 = 48 / 3 = 16 см;
b = S / h2 = 48 / 4 = 12 см.
Периметр параллелограмма равен сумме длин всех его сторон:
P = 2 * (a + b) = 2 * (16 + 12) = 2 * 28 = 56 см.( 16+16+12+12=56)
Ответ: периметр параллелограмма -56см.
Пояснення: