Предмет: Алгебра,
автор: kindratkoulia
розв'яжіть нерівність
Приложения:
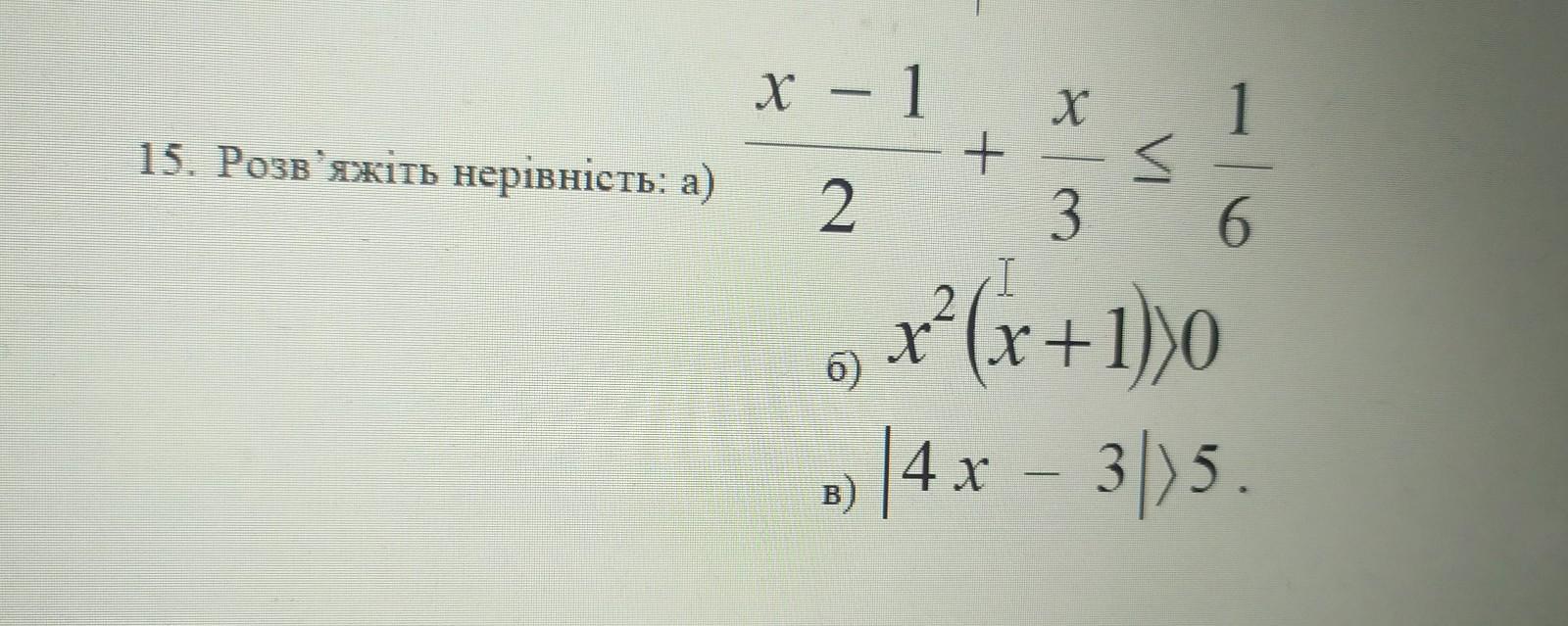
Ответы
Автор ответа:
2
Решение .
Решить неравенства .
1) Умножим неравенство на 6 , чтобы освободиться от знаменателя .
Ответ: .
2) Метод интервалов решения неравенств .
3) Неравенство с модулем .
Правило :
Так как записана совокупность неравенств ( не система неравенств) , то объединяем полученные множества решений :
Ответ: .
Похожие вопросы
Предмет: История,
автор: sanya4292
Предмет: Математика,
автор: neznayyyka0000
Предмет: Алгебра,
автор: neznayyyka0000
Предмет: Математика,
автор: ndrvkk
Предмет: Английский язык,
автор: GhostFox013