Предмет: Геометрия,
автор: pbaddy4
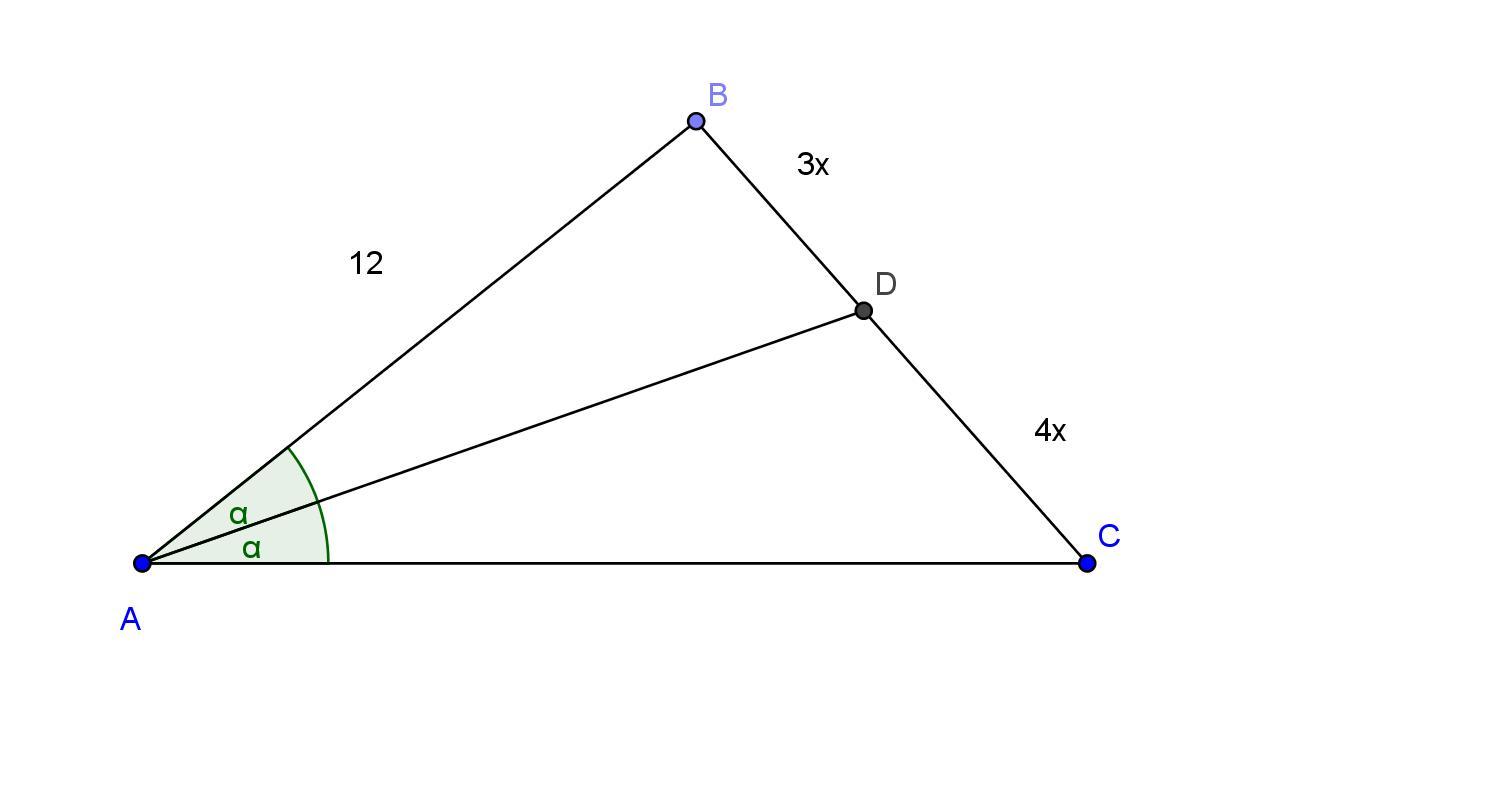
биссектриса угла A треугольника ABC делит сторону BC в отношении 3:4, считая от вершишны B. Если AB= 12, то найдите длину стороны AC
С решением
antonovm:
12 / AC = 3 / 4
Ответы
Автор ответа:
0
Ответ:
AC=16
Объяснение:
Теорема о биссектрисе треугольника:
Биссектриса треугольника делит противоположную сторону треугольника на два отрезка, длины которых пропорциональны соответствующим прилежащим сторонам треугольника.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: PradunDaria
Предмет: Алгебра,
автор: oksanasarana2017
Предмет: Английский язык,
автор: Аноним
Предмет: Алгебра,
автор: aleeexshadow