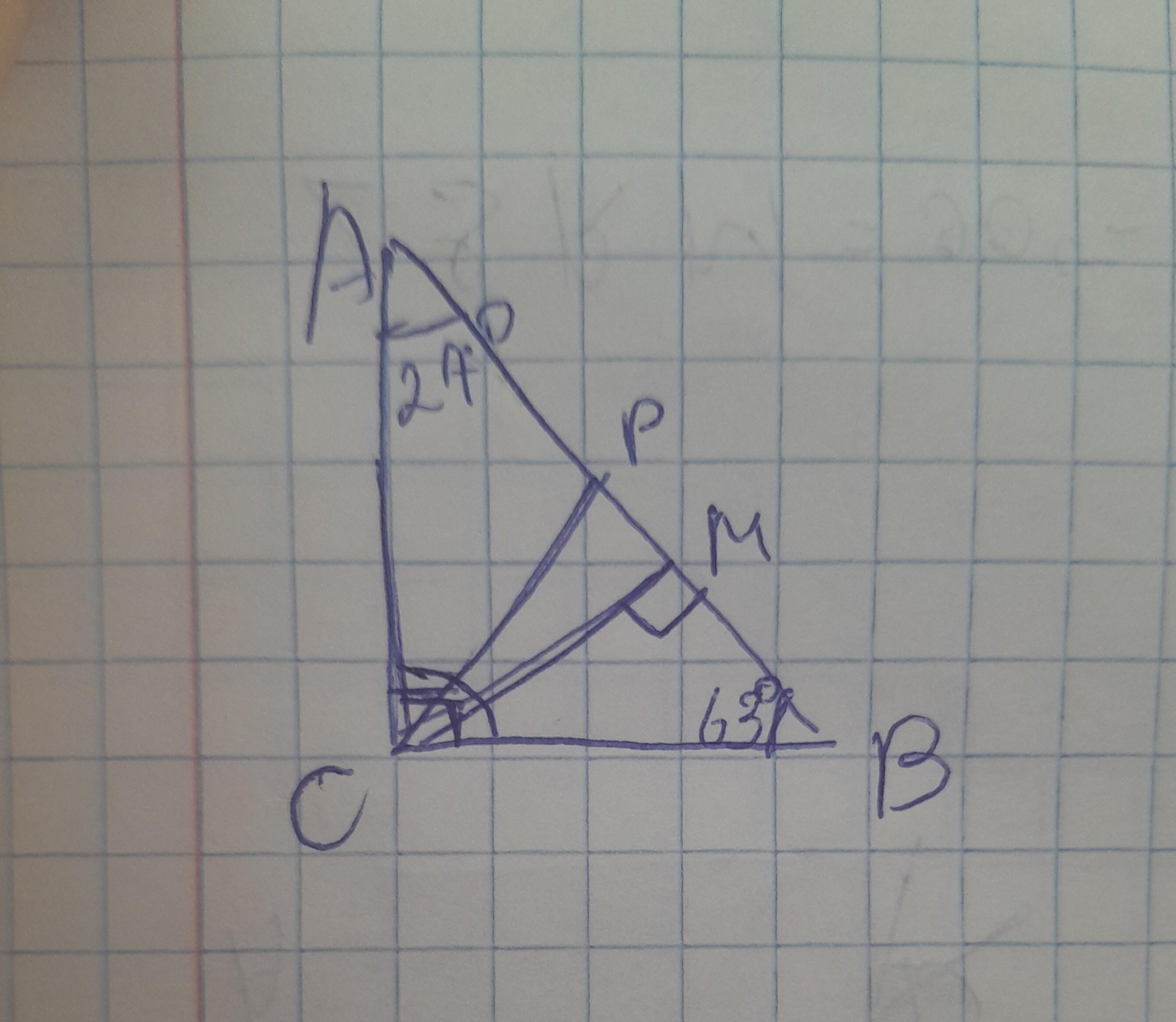Question

45 БАЛЛОВ ГЕОМЕТРИЯ 8 КЛАСС. ЛЕГКАЯ ЗАДАЧКА, ЛЕГКИЕ 45 БАЛЛОВ

Answer 1

Відповідь:  

Д)-18°

Дано:

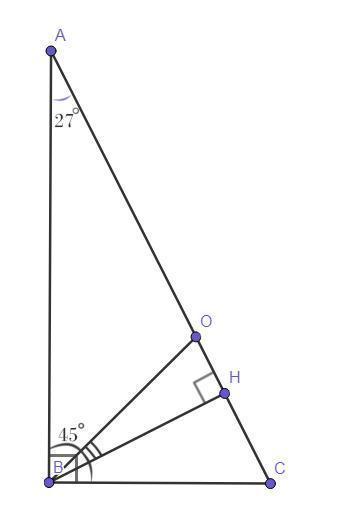
ΔАВС - прямоугольный,∠В = 90°;                                                                      ВО - биссектриса ∠В в прямоугольном ΔАВС; ВН - высота.

∠А = 27°.

Найти:

∠ОВН = ?

Решение:

Рассмотрим ΔВАН - прямоугольный (так как ВН⊥АС).

Сумма острых углов прямоугольного треугольника равна 90°.

∠ВАО+∠АВН = 90°;∠АВН = 90°-∠ВАО;∠АВН = 90°-27°;∠АВН = 63°.

Рассмотрим ∠В. Так как отрезок ВО - биссектриса, то ∠АВО = ∠ОВС = 90°/2 = 45° (по определению биссектрисы).

Рассмотрим ∠АВН.

∠АВН = ∠АВО+∠ОВН; ∠ОВН = ∠АВН-∠АВО;∠ОВН = 63°-45°;∠ОВН = 18°.

Ответ: 18°.

Пояснення:

Answer 2

Ответ:

18°

Объяснение:

кут В = 90° - 27° = 63° — за вл. гострих кутів прямок. трикутника

кут MCB = 90° - 63° = 27°

кут PCB = 1/2 кута С = 45° – за вл. бісектриси

кут МСР = 45° - 27° = 18°