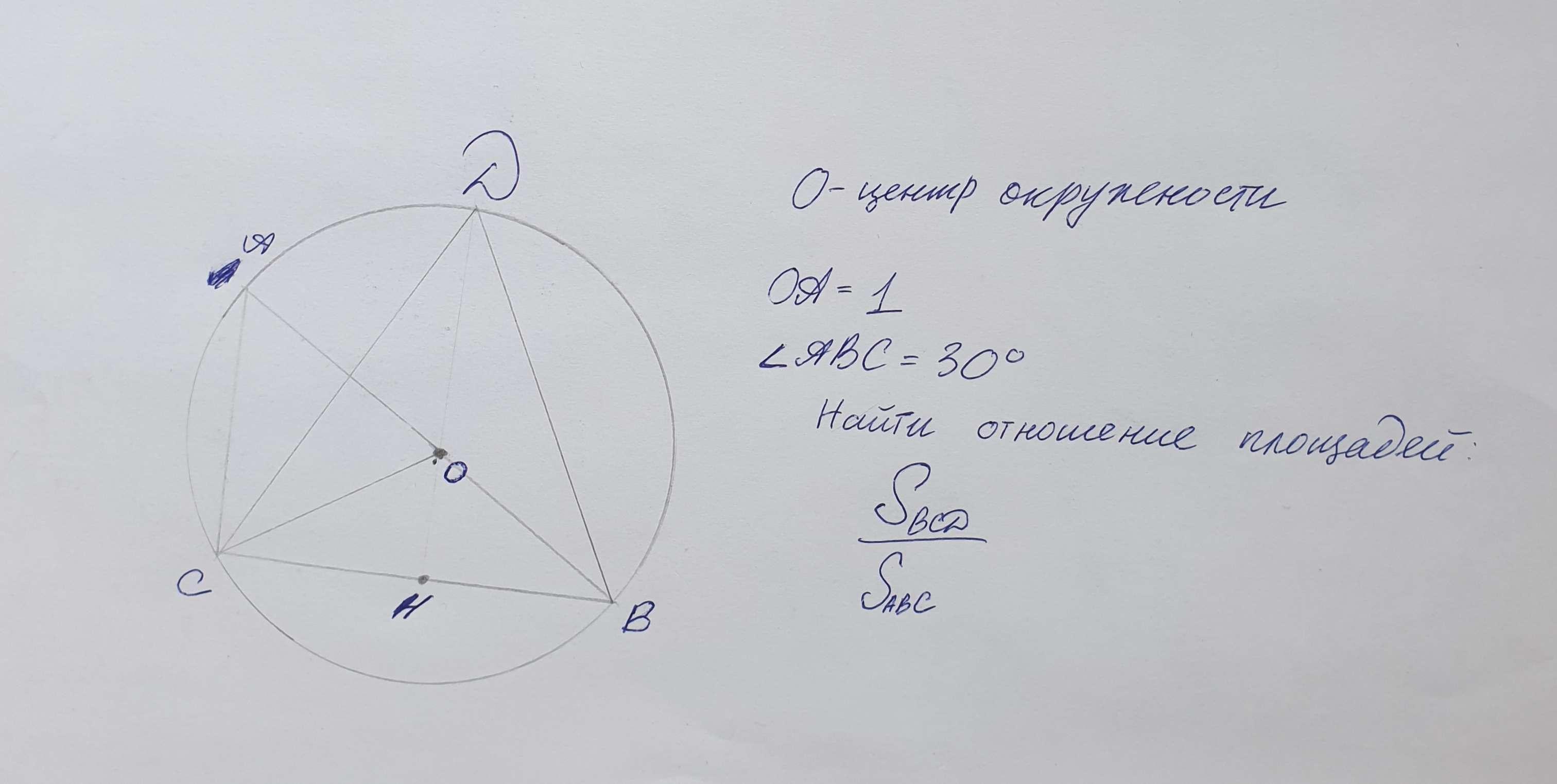
Всё во вложении, подробно обьяснить
Ответы
Ответ:
3
Объяснение:
1)Вписанный угол ABC опирается на дугу AC, как и центральный угол AOC => AOC=2*ABC=60°.
Поскольку AOC-равнобедренный(AO=OC радиусы), то угол CAO=OCA=(180-AOC)/2=60°.
2) Угол CAO=CDB=60°(опираются на одну дугу), кроме того CDB-равнобедренный(так как высота DH проходит через центр описанной окружности, то серединный перпендикуляр совпадает с DH, то есть DH ещё и медиана), следовательно, углы DCB и DBC так же равны по 60°
3)Треугольники CDB и AOC подобны( их углы равны) и отношение площадей есть коэффициент подобия в квадрате, BC найдём рассмотрев прямоугольный треугольник ACB(один из углов опирается на диаметр)
Объяснение:
АВ=2•ОА=2•1=2
Вписанный угол опирающийся на диаметр окружности - прямой , значит ∠АСВ - прямой.
∆АВС - прямоугольный:
Катет лежащий против угла 30° равен половине гипотенузы:
АС=АВ:2=2:2=1
по теореме Пифагора:
ВС=√(АВ²-АС²)=√(2²-1²)=√3
S(ABC)=1/2•AC•BC=1/2•1•√3=√3/2
Pассмотрим ∆ВОС - равнобедреный,где
ОС=ОВ=ОА=1 - как радиусы.
Проведем высоту ОН, которая равнобдренном треугольнике является медианой и биссектрисой:
∆ОНВ - прямоугольный:
катет лежащий против угла 30° равен половине гипотенузы: ОН=ОВ:2=1/2
DH=OH+DO=1/2+1=3/2 ,где DO=OA=1 - радиус
∆СDH=∆BDH - по 2 катетам, значит
соответственные элементы равны, следовательно, СD=DB . отсюда ∆ВСD - равнобедреный : DH - высота.
S(BCD)=1/2•CB•DH=1/2•√3•3/2=(3√3)/4
S(BCD)/S(ABC)=((3√3)/4)/(√3/2)=
=((3√3)/4)•(2/√3)=3/2=1,5
ответ: S(BCD)/S(ABC)=1,5