Предмет: Алгебра,
автор: serezha544
Количество действительных решений уравнения 2×3^3х -15 ×9^х+24×3^х+16= 0 равно выберите один ответ СРОЧНО
3
0
4
1
2
tamarabernukho:
2×3^(3х) -15 ×9^х+24×3^х+16= (3^x-4)²(2*3^x+1)=0
3^x=4;x=log(3,4)
Ответы
Автор ответа:
2
Ответ:
Показательное уравнение .
Сделаем замену : . Тогда получим уравнение :
Если уравнение имеет целые корни, то они являются делителями числа 16/2 = 8 . Проверим делитель числа 8 число y = 4 . Можно сначала и другие делители проверять, но они не дадут результат. Подставим y = 4 в уравнение:
.
Так как получили 0 , то y = 4 является корнем уравнения . Можно разделить на разность (y-4) , получим многочлен 2 степени .
Теперь найдём корни квадратного трёхчлена .
Окончательно получаем
Перейдём к старой переменной .
уравнение не имеет решений , так как
.
Ответ: количество действительных решений равно одному , и это
.
Приложения:


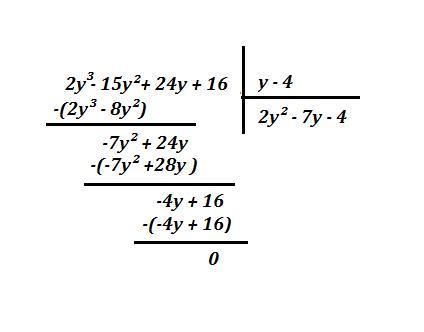
вы здесь?
Похожие вопросы
Предмет: Алгебра,
автор: sasakapustnik88
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: vadimpaveliev2004
Предмет: Физика,
автор: visitors48
Предмет: Английский язык,
автор: Arxangel37711