Предмет: Алгебра,
автор: lor3xgames
ТЕРМІНОВО БУДЬЛАСКА ДОПОМОЖІТЬ
Приложения:
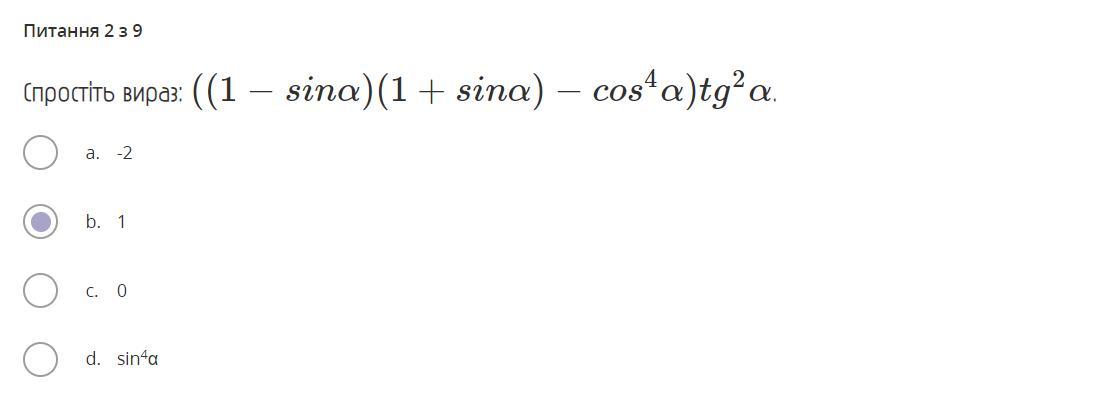


Sanoc22057:
Напиши це словами
Ответы
Автор ответа:
1
Ответ:
1) Применяем формулу разности квадратов, основные тригонометрические тождества .
2) Вычислить значения выражения . Применяем свойства степеней
3) Наибольшее значение функции равно 6 , так как
Приложения:

Автор ответа:
0
Відповідь:
Пояснення:
розв'язання завдання додаю
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: fruitandbloxs
Предмет: Английский язык,
автор: kuanastasia615
Предмет: Геометрия,
автор: sgwrgwrgrqgwdgfsdfss
Предмет: Математика,
автор: FelixxxPRO
Предмет: Математика,
автор: Аноним