Предмет: Алгебра,
автор: lubluglenna
помогите пожалуйста с системой тригонометрических уравнений
Приложения:
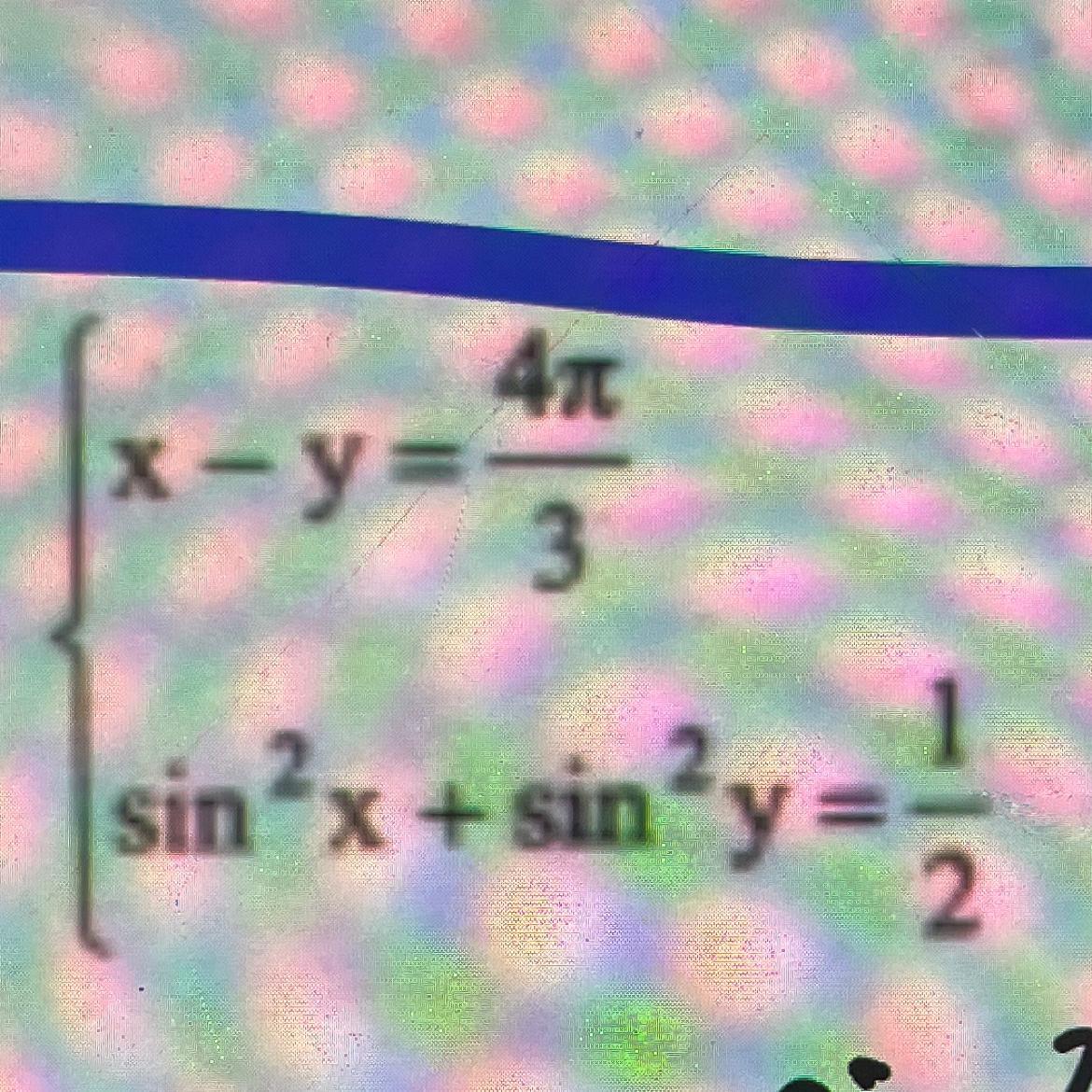
yevheniiavz:
Вы бы хоть смотрели внимательней, далеко не одно и то же
Ну, вы сделали всё тоже самое с синусами, что я с косинусами
https://ibb.co/hBMFz2R
ну конечно надо было понизить степень , зачем эти квадраты ?
По ссылки не переходит...
попробуйте в другом браузере
в хроме всё переходит
скопируйте ссылку и откройте в посковике
поисковике
Да, вижу теперь. Хорошее решение! Не догадался понизить степень
Ответы
Автор ответа:
1
Автор ответа:
1
...................................
Приложения:

Фактически одно и тоже решение, что у меня...
Вот именно, что "фактически". Начало да, похожее, согласен. А дальше идёт решение совсем по-другому
Да нет, вы свели к стандартному виде однородного уравнения и после перешли к тангенсу, а я этого не сделал и сразу перешёл к тангенсу, получили потом одно и тоже. Да ладно, я же без агрессии какой-либо
Так я тоже :) вы сами сейчас подтвердили, что ваше решение ≠ моему. А "получили потом одно и тоже" - логично, ибо ответ конечный разным быть не может.
Нет, я не про ответ, а про то, что получился тангенс такой же. Можно одно и тоже уравнение решать по разному и получить по виду разные ответы, а так они будут одинаковые. Знаете, это когда ты получаешь корень pi/6, хочешь проверить по вольфраму, а он выдаёт какой-нибудь такой корень arctg(sqrt(1-sqrt(2)))+2pik, например) То есть, калькулятор делал максимально в лоб, но ответы у вас одинаковые)
Похожие вопросы
Предмет: Українська мова,
автор: Mamaamakriminal22
Предмет: Физика,
автор: KirillTrackor
Предмет: Математика,
автор: screan91148
Предмет: Математика,
автор: ustinovat17
Предмет: Алгебра,
автор: slava20035