Question

Пожалуйста срочно!!!
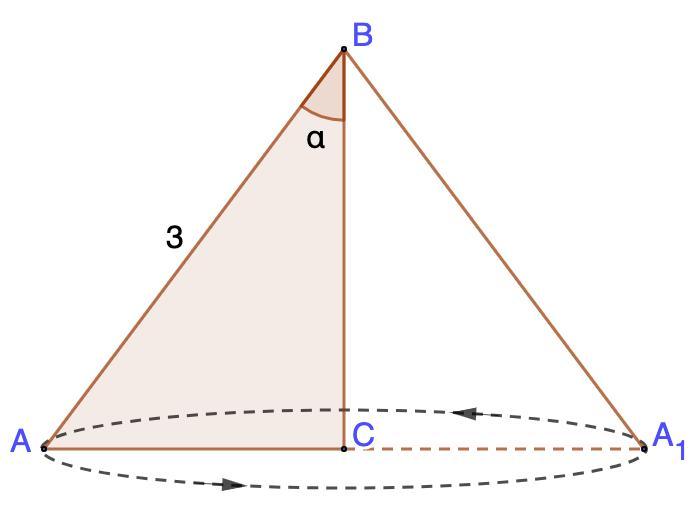
В прямоугольном треугольнике АВС гипотенуза АВ равна 3, угол А равен а. Треугольник АВС вращается вокруг катета ВС. Найдите объем полученного тела вращения

Answer 1

Ответ:

Объем полученного тела вращения равен 9π sin²α cosα.

Пошаговое объяснение:

В прямоугольном треугольнике АВС гипотенуза АВ равна 3, угол А равен α. Треугольник АВС вращается вокруг катета ВС. Найдите объем полученного тела вращения.

Дано: ΔАВС - прямоугольный;

АВ = 3 - гипотенуза;

∠А = α;

ΔАВС вращается вокрук ВС.

Найти: объем полученного тела вращения.

Решение:

Полученное тело вращения - конус с радиусом основания АС и  высотой ВС.

• Объем конуса равен:

          V = 1/3 · Sосн. · h,

где Sосн. - площадь основания конуса, h - его высота.

Рассмотрим ΔАВС - прямоугольный.

• Синус угла  - отношение противолежащего катета к гипотенузе.

$\displaystyle sin\;\alpha = \frac{AC}{AB}\;\;\;\Rightarrow \;\;\;AC=AB\cdot sin\;\alpha = 3sin\;\alpha$

• Косинус угла  - отношение прилежащего катета к гипотенузе.

$\displaystyle cos\;\alpha = \frac{BC}{AB}\;\;\;\Rightarrow \;\;\;BC=AB\cdot cos\;\alpha = 3cos\;\alpha$

• Площадь круга равна:

          Sосн. = πR²,

где R - радиус основания.

⇒ Sосн. = π · АС² = π · 9sin²α = 9π sin²α

Найдем объем конуса:

V = 1/3 · 9π sin²α · 3 cos α = 9π sin²α cosα

Объем полученного тела вращения равен 9π sin²α cosα.