Предмет: Геометрия,
автор: ushd42
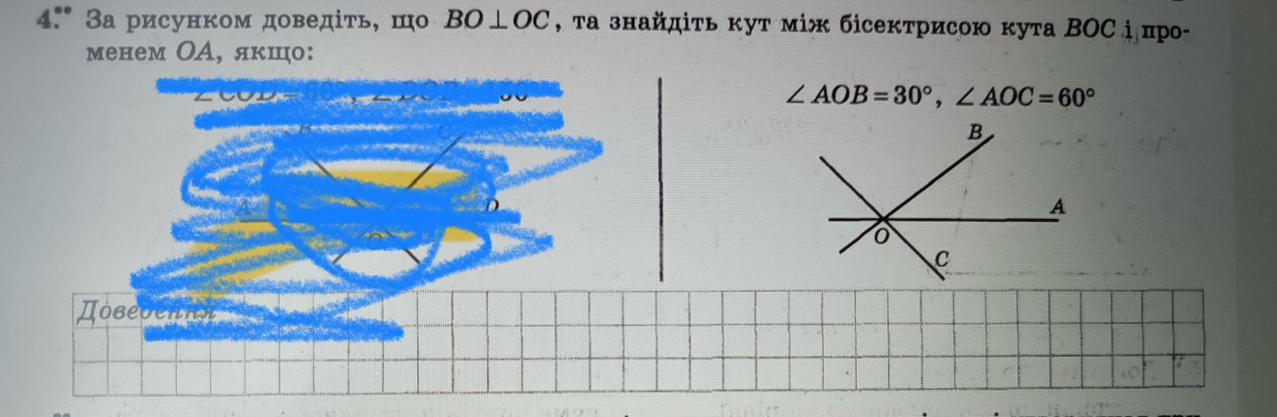
За рисунком доведіть, що ВО 1ОС, та знайдіть кут між бісектрисою кута ВОС і про-
менем ОА, якщо:
L AOB=30°, LAOC= 60°
Швидко з розгорнутою відповіддю
Приложения:
Ответы
Автор ответа:
3
Найдём угол BOC, так как он связан с прямыми BO и OC:
∠BOC = ∠AOC + ∠BOA
∠BOC = 30° + 60°
∠BOC = 90°
Так как ∠BOC - прямой (равен 90°), то все остальные углы, смежные с ним и вертикальный ему, также равны 90°:
∠COB1 = ∠BOB1 - BOC = 180° - 90° = 90° ; и также про другие углы.
Из этого следует, что ВО перпендикулярна ОС, так как уже один угол между ними равен 90°.
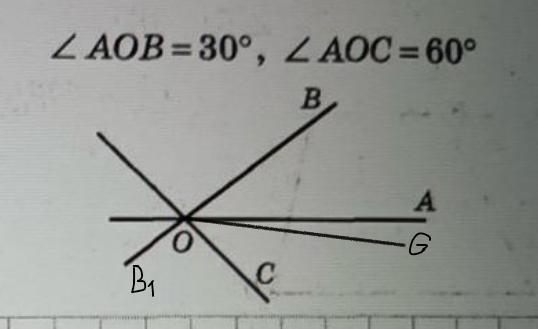
Биссектриса угла ВОС = ∠BOC : 2. Дорисуем на рисунке ещё одну прямую, обозвав G, чтобы обозначить биссектрису. У нас получились ∠BOG = ∠CОG (так как OG - биссектриса)
∠COG = ∠BOC : 2 = 90° : 2 = 45°
Чтобы найти угол (∠AOG) между биссектрисой OG и OA:
∠BOC = ∠BOA + ∠AOG + ∠COG
∠AOG = ∠BOC - ∠BOA -∠COG
∠AOG = 90° - 30° - ∠45°
∠AOG = 15°
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Информатика,
автор: petrgoi228
Предмет: Математика,
автор: Ihelpissl
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: strelnikovaana05